以2l为周期的函数的傅里叶级数
设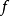 是以
是以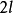 为周期的函数,则其傅里叶系数为
为周期的函数,则其傅里叶系数为
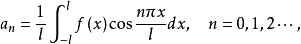
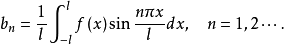
所以,其傅里叶级数为
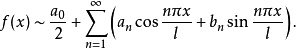
若函数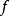 在
在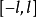 上按段光滑,则由收敛定理得1
上按段光滑,则由收敛定理得1
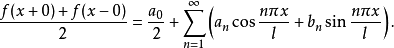
正弦级数与余弦级数奇函数的傅里叶级数—正弦函数设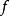 是以
是以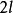 为周期的奇函数,或是定义在
为周期的奇函数,或是定义在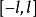 上的奇函数,则在
上的奇函数,则在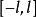 上,
上,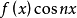 是奇函数,
是奇函数,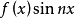 是偶函数。因此,
是偶函数。因此,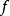 的傅里叶系数是1
的傅里叶系数是1
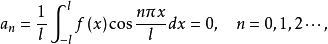
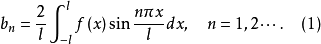 所以当
所以当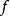 为奇函数时,它的傅里叶级数只含有正弦函数的项,即
为奇函数时,它的傅里叶级数只含有正弦函数的项,即
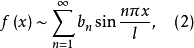 其中
其中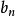 如(1)所示。(2)式右边的级数称为正弦级数。
如(1)所示。(2)式右边的级数称为正弦级数。
当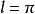 ,则奇函数
,则奇函数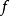 所展开成的正弦级数为
所展开成的正弦级数为
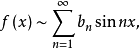 其中
其中
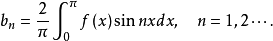
偶函数的傅里叶级数—余弦级数设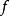 是以
是以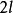 为周期的偶函数,或是定义在
为周期的偶函数,或是定义在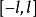 上的偶函数,则在
上的偶函数,则在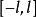 上,
上,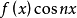 是偶函数,
是偶函数,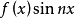 是奇函数。因此,
是奇函数。因此,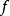 的傅里叶系数是1
的傅里叶系数是1


于是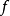 的傅里叶级数只含有余弦函数的项,即
的傅里叶级数只含有余弦函数的项,即
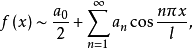 其中
其中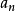 如(3)所示。(4)式右边的级数称为余弦级数。
如(3)所示。(4)式右边的级数称为余弦级数。
当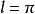 ,则偶函数
,则偶函数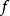 所展开成的余弦函数为
所展开成的余弦函数为
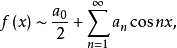 其中
其中
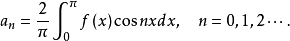
应用定义在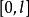 上的函数
上的函数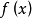 展成正弦级数。
展成正弦级数。
具体步骤2:
(1)奇延拓:在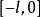 上补充定义得
上补充定义得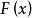 ,使得
,使得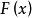 在
在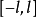 为奇函数。
为奇函数。
(2)对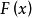 作周期延拓。
作周期延拓。
(3)将经过奇延拓与周期延拓后的函数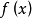 展成傅里叶级数
展成傅里叶级数
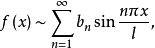 其中
其中
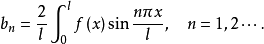 定义在
定义在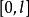 上的函数
上的函数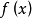 展成余弦级数。
展成余弦级数。
具体步骤:2
(1)偶延拓:在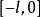 上补充定义得到
上补充定义得到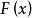 ,使得
,使得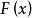 在
在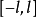 为偶函数。
为偶函数。
(2)对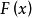 作周期延拓。
作周期延拓。
(3)将经过偶延拓与周期延拓后的函数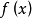 展成傅里叶级数
展成傅里叶级数
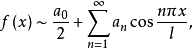
其中
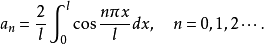




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国