概念
散度定理是指在向量分析中,一个把向量场通过曲面的流动(即通量)与曲面内部的向量场的表现联系起来的定理。更加精确地说,散度定理说明向量场穿过曲面的通量,等于散度在曲面围起来的体积上的积分。直观地,所有源点的和减去所有汇点的和,就是流出这区域的净流量。
高斯公式在工程数学中是一个很重要的结果,特别是静电学和流体力学。
在物理和工程中,散度定理通常运用在三维空间中。然而,它可以推广到任意维数。在一维,它等价于微积分基本定理;在二维,它等价于格林公式。
这个定理是更一般的斯托克斯公式的特殊情形。
定理设空间闭区域Ω是由分片光滑的闭曲面Σ所围起来的三维区域,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在Ω上具有一阶连续偏导数,则有
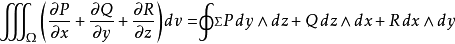
或
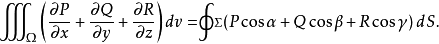
这里Σ是Ω的边界(boundary),cos α、cos β、cos γ是Σ在点(x,y,z)处的单位法向量的方向余弦。
这两个公式都叫做高斯公式,不过这两公式仅仅是表达方式不同,其实是相同的定理,这可以用变数变换得到两公式的右边都等于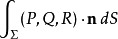 ,其中
,其中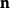 是曲面
是曲面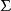 的向外单位法向量1。
的向外单位法向量1。
表示方法用散度表示高斯公式用散度表示为:
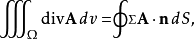 其中Σ是空间闭区域Ω的边界曲面,而
其中Σ是空间闭区域Ω的边界曲面,而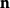 是曲面Σ上的朝外的单位法向量。
是曲面Σ上的朝外的单位法向量。
用向量表示令V代表有一间单闭曲面S为边界的体积,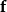 是定义在V中和S上连续可微的向量场。如果
是定义在V中和S上连续可微的向量场。如果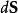 是外法向向量面元,则
是外法向向量面元,则
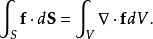
推论对于标量函数g和向量场F的积,应用高斯公式可得:

对于两个向量场{\displaystyle \mathbf {F} \times \mathbf {G} }的向量积,应用高斯公式可得:
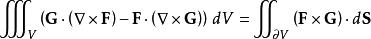
对于标量函数f和非零常向量的积,应用高斯公式可得:
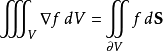
对于向量场F和非零常向量的向量积,应用高斯公式可得:
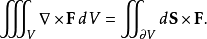
例子假设我们想要计算 其中S是一个单位球面,定义为
其中S是一个单位球面,定义为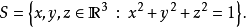 F是向量场:
F是向量场: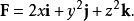
直接计算这个积分是相当困难的,但我们可以用高斯公式来把它简化:
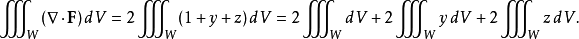
其中W是单位球: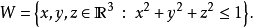
由于函数y和z是奇函数,我们有: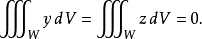
因此:
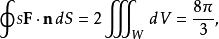
因为单位球W的体积是4π3.
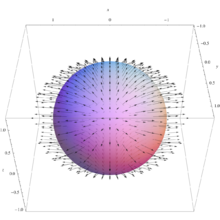
说明:例子所对应的向量场。注意,向量可能指向球面的内侧或者外侧。
二阶张量的散度定理二阶张量的高斯公式实际上是上面的高斯公式的推论。为了使内容完整,首先简要地介绍三维欧几里得空间上的二阶张量(详见并矢张量或张量积)以及相关的概念和记号2。在这里,向量和向量场用黑斜体字母表示,张量用正黑体字母表示。
1)两个向量a和b并排放在一起所形成的量ab被称为向量a和b的并矢或并矢张量。注意,一般来说 .
.
2)ab=0的充分必要条件是a=0或b=0。
3)二阶张量就是有限个并矢的线性组合。
4)ab分别线性地依赖于a和b。
5)二阶张量T和向量a的缩并T*a以及a*T对, T和a都是线性的。
6)特别是,当T=uv时,

所以,一般来说,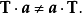 。
。
定理:
设V是三维欧几里得空间中的一个有限区域,S是它的边界曲面,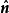 是S的外法线方向上的单位向量,T是定义在V的某个开邻域上
是S的外法线方向上的单位向量,T是定义在V的某个开邻域上 的连续的二阶张量场,
的连续的二阶张量场,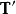 是T的转置,则
是T的转置,则
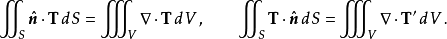




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国