[科普中国]-平面连杆机构-

平面连杆机构是由若干构件用低副(转动副、移动副)连接组成的平面机构。最简单的平面连杆机构由四个构件组成，称为平面四杆机构。平面连杆机构广泛应用于各种机械、仪表和各种机电产品中。1

特点平面连杆机构广泛应用于各种机械和仪表中，其主要优点有：

1)由于连杆机构中的运动副都是面接触的低副，因而承受的压强小，便于润滑，磨损较轻，承载能力高；

2)构件形状简单，加T方便，构件之问的接触是由构件本身的几何约束来保持的，故构件工作可靠；

3)可实现多种运动形式之间的变换：

4)利用连杆可实现多种运动轨迹的要求。

其缺点有：

1)低副中存在间隙，构件数目较多时会产生较大的累积运动误差，从而降低运动精度，效率低；

2)机构运动时产生的惯性力难以平衡，故不适宜于高速场合。2

分类平面连杆机构的类型很多，从组成机构的杆件数来看有四杆机构、五杆机构和六杆机构等，一般将由五个或五个以上的构件组成的连杆机构称为多杆机构。3

基本类型平面铰链四杆机构根据其两连架杆的运动形式不同，可分为双曲柄机构、曲柄摇杆机构和双摇杆机构三种基本形式。

双曲柄机构连架杆均为曲柄的四杆机构，称为双曲柄机构。图8.3所示的惯性筛机构是双曲柄机构。它由曲柄1、3、连杆2、5、机架4和筛6组成，当曲柄1等速回转时，另一曲柄3变速回转，使筛6具有所需的加速度，利用加速度所产生的惯性力，使物料在筛上往复运动而达到筛选的目的。4

曲柄摇杆机构两连架杆中一个为曲柄，另一个为摇杆的四杆机构，称为曲柄摇杆机构。图8.4所示的雷达天线俯仰角调整机构就是曲柄摇杆机构。天线固定在连架摇杆3上，由主动曲柄1通过连杆2使天线缓缓摆动，要求实现一定的摆角，以保证天线具有指定的摆动角。4

双摇杆机构两连架杆均为摇杆的四杆机构称为双摇杆机构。图8.5所示的汽车前轮转向机构就是双摇杆机构。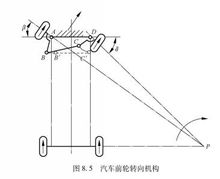

曲柄存在条件(1)连架杆或机架为最短杆；

(2)最短杆与最长杆长度之和小于或等于其他两杆长度之和。

在有整转副即曲柄存在的铰链四杆机构中，最短杆两端的转动副均为整转副，因此：若取最短杆为机架，则得双曲柄机构；若取最短杆的任一相邻的构件为机架，则得曲柄摇杆机构；若取最短杆对边为机架，则得双摇杆机构。

若铰链四杆机构最短杆与最长杆长度之和大于其他两杆长度之和，则无曲柄存在，两连架杆均为摇杆。但此时这种情况下形成的双摇杆机构与上述双摇杆机构不同，它不存在整转副。

平面四杆机构简介低副是面接触，耐磨损；加上转动副和移动副的接触表面是圆柱面和平面，制造简便，易于获得较高的制造精度。因此，平面连杆机构在各种机械和仪器中获得广泛应用。连杆机构的缺点是：低副中存在间隙，数目较多的低副会引起运动累积误差；而且它的设计比较复杂，不易精确地实现复杂地运动规律。

最简单的平面连杆机构是由四个构件组成的，称为平面四杆机构。它的应用非常广泛，而且是组成多杆机构的基础。

由若干个刚性构件通过低副(转动副、移动副)联接，且各构件上各点的运动平面均相互平行的机构（图1），又称平面低副机构。低副具有压强小、磨损轻、易于加工和几何形状能保证本身封闭等优点，故平面连杆机构广泛用于各种机械和仪器中。与高副机构相比，它难以准确实现预期运动，设计计算复杂。

平面连杆机构中最常用的是四杆机构，它的构件数目最少，且能转换运动。多于四杆的平面连杆机构称多杆机构，它能实现一些复杂的运动，但杆多且稳定性差。

运动设计基本问题平面连杆机构的运动设计一般可归纳为以下三类基本问题：

1) 实现构件给定位置（亦称刚体导引），即要求连杆机构能引导某构件按规定顺序精确或近似地经过给定的若干位置。

2) 实现已知运动规律（亦称函数生成），即要求主、从动件满足已知的若干组对应位置关系，包括满足一定的急回特性要求，或者在主动件运动规律一定时，从动件能精确或近似地按给定规律运动。

3) 实现已知运动轨迹（亦称轨迹生成），即要求连杆机构中作平面运动的构件上某一点精确或近似地沿着给定的轨迹运动。

在进行平面连杆机构运动设计时，往往是以上述运动要求为主要设计目标，同时还要兼顾一些运动特性和传力特性等方面的要求，如整转副要求、压力角或传动角要求、机构占据空间位置要求等。另外，设计结果还应满足运动连续性要求，即当主动件连续运动时，从动件也能连续地占据预定的各个位置，而不能出现错位或错序等现象。

平面连杆机构运动设计的方法主要是几何法和解析法，此外还有图谱法和模型实验法。几何法是利用机构运动过程中各运动副位置之间的几何关系，通过作图获得有关运动尺寸，所以几何法直观形象，几何关系清晰，对于一些简单设计问题的处理是有效而快捷的，但由于作图误差的存在，所以设计精度较低。解析法是将运动设计问题用数学方程加以描述，通过方程的求解获得有关运动尺寸，故其直观性差，但设计精度高。随着数值计算方法的发展和计算机的普及应用，解析法已成为各类平面连杆机构运动设计的一种有效方法。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院