[科普中国]-维特比算法

维特比算法是一种动态规划算法用于寻找最有可能产生观测事件序列的-维特比路径-隐含状态序列，特别是在马尔可夫信息源上下文和隐马尔可夫模型中。术语“维特比路径”和“维特比算法”也被用于寻找观察结果最有可能解释相关的动态规划算法。例如在统计句法分析中动态规划算法可以被用于发现最可能的上下文无关的派生(解析)的字符串，有时被称为“维特比分析”。

来源维特比算法由安德鲁·维特比(Andrew Viterbi)于1967年提出，用于在数字通信链路中解卷积以消除噪音。 此算法被广泛应用于CDMA和GSM数字蜂窝网络、拨号调制解调器、卫星、深空通信和802.11无线网络中解卷积码。现今也被常常用于语音识别、关键字识别、计算语言学和生物信息学中。例如在语音(语音识别)中，声音信号作为观察到的事件序列，而文本字符串，被看作是隐含的产生声音信号的原因，因此可对声音信号应用维特比算法寻找最有可能的文本字符串。1

算法假设给定隐式马尔可夫模型（HMM）状态空间 S，共有k个状态，初始状态i的概率为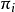 ，从状态 i 到状态 j 的转移概率为 。 令观察到的输出为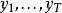 。 产生观察结果的最有可能的状态序列 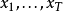由递推关系给出：

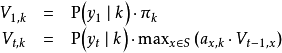
此处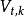 是前 t 个最终状态为 k 的观测结果最有可能对应的状态序列的概率。 通过保存向后指针记住在第二个等式中用到的状态 x 可以获得维特比路径。声明一个函数 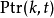，它返回若 时计算 用到的 x 值 或若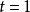 时的 k，这样:

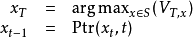
这里我们使用了arg max的标准定义 算法复杂度为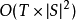 。1

算法基础维特比算法的基础可以概括成下面三点：

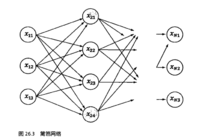1.如果概率最大的路径p(或者说最短路径)经过某个点，比如途中的X22，那么这条路径上的起始点S到X22的这段子路径Q，一定是S到X22之间的最短路径。否则，用S到X22的最短路径R替代Q，便构成一条比P更短的路径，这显然是矛盾的。证明了满足最优性原理。

2.从S到E的路径必定经过第i个时刻的某个状态，假定第i个时刻有k个状态，那么如果记录了从S到第i个状态的所有k个节点的最短路径，最终的最短路径必经过其中一条，这样，在任意时刻，只要考虑非常有限的最短路即可。

3. 结合以上两点，假定当我们从状态i进入状态i+1时，从S到状态i上各个节的最短路径已经找到，并且记录在这些节点上，那么在计算从起点S到第i+1状态的某个节点Xi+1的最短路径时，只要考虑从S到前一个状态i所有的k个节点的最短路径，以及从这个节点到Xi+1，j的距离即可。1

C++代码实现#include #include #include using namespace std;int main(){ double pi[3] = { 0.2, 0.4, 0.4 }; double C[3][3] = { 0.5, 0.2, 0.3, 0.3, 0.5, 0.2, 0.2, 0.3, 0.5 }; double E[3][2] = { 0.5, 0.5, 0.4, 0.6, 0.7, 0.3 }; string output[4] = { "R", "W", "R","W" }; int state[3] = { 1, 2, 3 }; int row = 3; int column = 3; //开辟数组空间 double **delta = new double *[row]; int **path = new int *[row]; int i, j,k; for (i = 0; i