拉格朗日定理存在于多个学科领域中,分别为:微积分中的拉格朗日中值定理;数论中的四平方和定理;群论中的拉格朗日定理 (群论)。
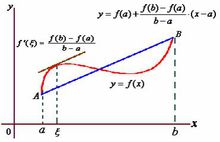
微积分在微积分中,拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形。
1.文字叙述如果函数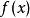 满足:1) 在闭区间
满足:1) 在闭区间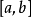 上连续;2) 在开区间
上连续;2) 在开区间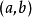 内可导;那么在
内可导;那么在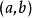 内至少有一点
内至少有一点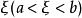 ,使等式
,使等式
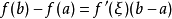 成立。
成立。
2.逻辑语言的叙述若函数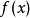 满足:
满足:
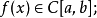
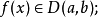 则
则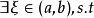
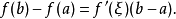
3.证明令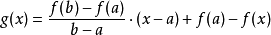 ,那么1
,那么1
1)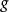 在
在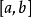 上连续,
上连续,
2)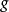 在
在 上可微(导),
上可微(导),
3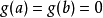 ,由罗尔定理,存在一点
,由罗尔定理,存在一点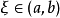 ,使得
,使得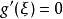 。即
。即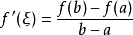 。
。
数论1.内容四平方和定理(Lagrange's four-square theorem) 说明每个正整数均可表示为4个整数的平方和。它是费马多边形数定理和华林问题的特例。注意有些整数不可表示为3个整数的平方和,例如7。
2.历史1. 1743年,瑞士数学家欧拉发现了一个著名的恒等式: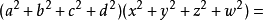
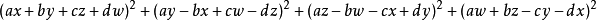 。根据上述欧拉恒等式或四元数的概念可知如果正整数
。根据上述欧拉恒等式或四元数的概念可知如果正整数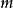 和
和 能表示为4个整数的平方和,则其乘积
能表示为4个整数的平方和,则其乘积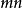 也能表示为4个整数的平方和。于是为证明原命题只需证明每个素数可以表示成4个整数的平方和即可。
也能表示为4个整数的平方和。于是为证明原命题只需证明每个素数可以表示成4个整数的平方和即可。
2. 1751年,欧拉又得到了另一个一般的结果。即对任意奇素数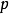 ,同余方程
,同余方程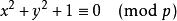 必有一组整数解
必有一组整数解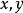 满足
满足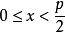 ,
,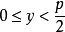 (引理一)。
(引理一)。
至此,证明四平方和定理所需的全部引理已经全部证明完毕。此后,拉格朗日和欧拉分别在1770年和1773年作出最后的证明。
群论拉格朗日定理是群论的定理,利用陪集证明了子群的阶一定是有限群的阶的约数值。
1.定理内容叙述:设H是有限群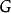 的子群,则
的子群,则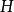 的阶整除
的阶整除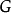 的阶。
的阶。
定理的证明是运用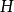 在
在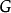 中的左陪集。
中的左陪集。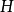 在
在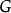 中的每个左陪集都是一个等价类。将
中的每个左陪集都是一个等价类。将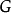 作左陪集分解,由于每个等价类的元素个数都相等,都等于
作左陪集分解,由于每个等价类的元素个数都相等,都等于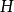 的元素个数(
的元素个数(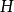 是
是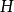 关于
关于 的左陪集),因此
的左陪集),因此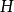 的阶(元素个数)整除
的阶(元素个数)整除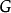 的阶,商是
的阶,商是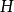 在
在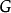 中的左陪集个数,叫做
中的左陪集个数,叫做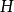 对
对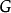 的指数,记作
的指数,记作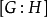 。
。
陪集的等价关系
定义二元关系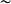 :
: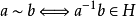 。下面证明它是一个等价关系。
。下面证明它是一个等价关系。
1) 自反性: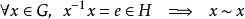 ;
;
2) 对称性: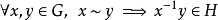 ,因此
,因此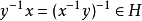 ,因此
,因此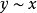 ;
;
3) 传递性: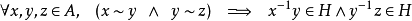 ,因此
,因此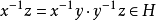 ,因此
,因此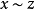 。
。
可以证明,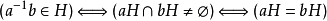 。因此左陪集是由等价关系
。因此左陪集是由等价关系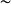 确定的等价类。
确定的等价类。
拉格朗日定理说明,如果商群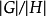 存在,那么它的阶等于
存在,那么它的阶等于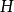 对
对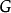 的指数
的指数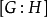 。
。
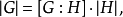 上述写法在为无限群时也成立。
上述写法在为无限群时也成立。
2.推论由拉格朗日定理可立即得到:由有限群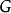 中一个元素
中一个元素 的阶数整除群
的阶数整除群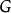 的阶(考虑由
的阶(考虑由 生成的循环群)。
生成的循环群)。
3.逆命题拉格朗日定理的逆命题并不成立。给定一个有限群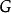 和一个整除
和一个整除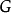 的阶的整数
的阶的整数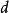 ,
,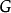 并不一定有阶数为
并不一定有阶数为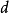 的子群。最简单的例子是4次交替群
的子群。最简单的例子是4次交替群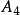 ,它的阶是12,但对于12的因数6,
,它的阶是12,但对于12的因数6,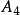 没有6阶的子群。对于这样的子群的存在性,柯西定理和西洛定理给出了一个部分的回答。
没有6阶的子群。对于这样的子群的存在性,柯西定理和西洛定理给出了一个部分的回答。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国