[科普中国]-沃尔泰拉积分方程

沃尔泰拉积分方程与弗雷德霍姆积分方程的不同之处，许多数学物理问题需通过积分方程或微分方程求解，积分方程是近代数学的一个重要分支。

定义形如

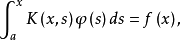
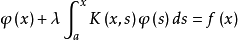的积分方程分别称为第一类和第二类沃尔泰拉积分方程，其中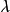， 是参数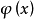， 是未知函数。这是沃尔泰拉（V.Volterra）在研究某个生态平衡问题时提出并讨论的积分方程。1

弗雷德霍姆积分方程形如

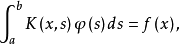
的积分方程分别称为第一类和第二类弗雷德霍姆积分方程。

其中，λ是参数，φ(x)是未知函数，。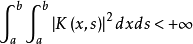

辨析第二类沃尔泰拉积分方程没有特征值，是区别于弗雷德霍姆积分方程的重要特点。对于任意的右端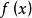，方程都有唯一解，并且解可以表示为

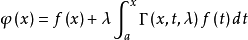其中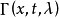， 为方程的解核。

沃尔泰拉积分方程与弗雷德霍姆积分方程的不同之处，仅在于它的积分上限是变量x，且α≤y≤x≤b，此处α、b是常量。沃尔泰拉积分方程可视为弗雷德霍姆积分方程的核K(x,y)当y>x时为零的情形。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学