[科普中国]-独立集

独立集是指图 G 中两两互不相邻的顶点构成的集合。任意有关图中团的性质都能很自然的转述成独立集的性质。一般而言，寻找图的最大团是 NP 困难的，从而寻找图的最大独立集也是 NP 困难的。但是，对于二部图的情形，有多项式时间算法找出图的最大独立集。

定义图的一一个顶点子集称为独立集，如果该子集中的任意两个项点在图中不相邻。图 G 的最大独立集所包含顶点的个数称作 G 的独立数(independence number)记作 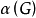。1

团在图论中，还有一个与独立集密切相关的概念——团。图的顶点子集称为团(clique)，如果该子集中的任意两个顶点在图中相邻。图 G 的最大团所包含顶点的个数称作 G 的团数(clique number)，记作 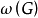。不难看出，一个图的团是其补图的独立集。因此，图的团数等于其补图的独立数，即 。

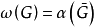任意有关图中团的性质都能很自然的转述成独立集的性质。一般而言，寻找图的最大团是 NP困难的,从而寻找图的最大独立集也是NP 困难的。但是，对于二部图的情形，有多项式时间算法找出图的最大独立集。

举例有个图有n个结点，y条边，任选图中一个顶点，把它染成黑色，则和它相连的顶点必须都被染成白色，但与被染成白色的顶点相连的顶点可以被染成白色也可以被染成黑色，问：这个图最多有多少个顶点能被染成黑色？

解：相当于求图的最大独立集。求一般图的最大独立集是NP hard。

具体程序实现可以通过求最小覆盖集来求最大独立集。

图G(V,E)的覆盖集D是顶点集的一个子集，并满足：任意 属于E，vi属于D或vj属于D。

定义 *，+ 满足交换率，结合率，且 * 对 + 分配 (a+b)*c = a*c + b*c

吸收率：a+ab = a，a*a = a，a+a = a

这样，求极小覆盖集：

M(连乘)(v[i] + M(所有与v[i]相邻的点))，i=0 to n

结果化简后的每个因子项即对应一个极小覆盖集。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学