垂足三角形(pedal triangle)是一种特殊三角形,指从三角形的三个顶点向对边作垂线段(即高),连结三个垂足所得的三角形。
定义垂足三角形是一种特殊三角形,指从三角形的三个顶点向对边作垂线段(即高),连结三个垂足所得的三角形。如图,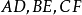 为
为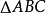 的高,则
的高,则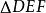 是
是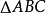 的垂足三角形,如果一个三角形的三个顶点分别在另一个三角形的三条边上,则该三角形称为另一个三角形的内接三角形,锐角三角形的垂足三角形必是它的内接三角形,在锐角三角形的所有内接三角形中,以垂足三角形的周长为最短,该问题称为施瓦兹三角形问题1。
的垂足三角形,如果一个三角形的三个顶点分别在另一个三角形的三条边上,则该三角形称为另一个三角形的内接三角形,锐角三角形的垂足三角形必是它的内接三角形,在锐角三角形的所有内接三角形中,以垂足三角形的周长为最短,该问题称为施瓦兹三角形问题1。
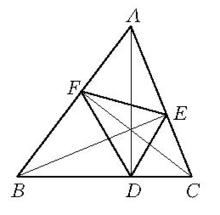
相关结论如图2,在锐角三角形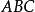 中,
中,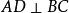 于D,
于D,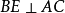 于E,
于E,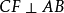 于F,则
于F,则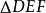 叫
叫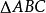 的垂足三角形。不难证明,原三角形的垂心是它的垂足三角形的内心:由
的垂足三角形。不难证明,原三角形的垂心是它的垂足三角形的内心:由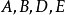 四点共圆,知
四点共圆,知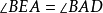 ,即
,即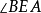 是
是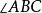 的余角。同理,由
的余角。同理,由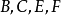 四点共圆,知
四点共圆,知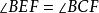 ,
,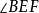 也是
也是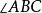 的余角,所以
的余角,所以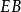 是
是 的平分线。同理
的平分线。同理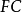 是
是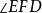 的平分线2。
的平分线2。
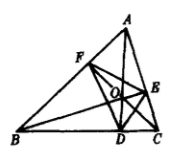
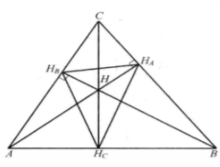
如图3,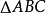 的垂心H的切瓦三角形(见下文)或称是它的射影三角形是垂足三角形(Orthic Triangle),也称为高线三角形,垂足
的垂心H的切瓦三角形(见下文)或称是它的射影三角形是垂足三角形(Orthic Triangle),也称为高线三角形,垂足 也是重心G的圆切瓦****三角形,如图33。
也是重心G的圆切瓦****三角形,如图33。
垂足三角形各顶点的三线坐标矩阵是
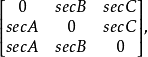 它的面积是
它的面积是
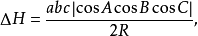 它的三条边长是
它的三条边长是
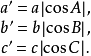 对于钝角和直角三角形,垂足三角形的半周长可以用下式表示
对于钝角和直角三角形,垂足三角形的半周长可以用下式表示
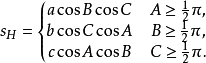 对于锐角三角形有一简化公式
对于锐角三角形有一简化公式
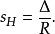
在锐角三角形中,任何内接三角形中以垂足三角形的周长最小。在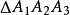 中,作出
中,作出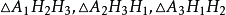 三个三角形的共轭重心
三个三角形的共轭重心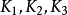 ,则它们分别在
,则它们分别在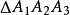 的三条中线上,如图4。
的三条中线上,如图4。
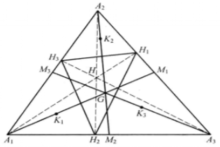
如果作出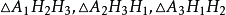 的欧拉线,则三条欧拉线交于一点,该点在
的欧拉线,则三条欧拉线交于一点,该点在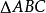 的九点圆上。若该点定为P,则下列等式中必有一个成立
的九点圆上。若该点定为P,则下列等式中必有一个成立
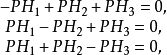
给定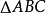 及其平面上,但不在三角形边上的一点P,联结
及其平面上,但不在三角形边上的一点P,联结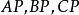 交对应边于
交对应边于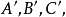 则
则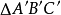 称为P点关于
称为P点关于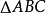 的切瓦三角形(Cevian Triangle),如图5。
的切瓦三角形(Cevian Triangle),如图5。

本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国