[科普中国]-面积坐标

三角形面积坐标是一种自然坐标，在有限元分析中一般用它来构造三角形单元的插值函数。随着有限元理论的发展，也出现了四边形单元的面积坐标等方法和理论。1

定义平面上任取一个⊿ABC，充当坐标三角形，对于平面ABC上任意一点M，将下述三角形面积比 S⊿MBC：S⊿AMC：S⊿ABM= ： ： 叫做点M关于⊿ABC的面积坐标(或重心坐标)，记作：M= ( ： ： )={ ， ， }。2

注：这里的面积 S⊿MBC，S⊿AMC，S⊿ABM都是有向面积。通常约定，顶点按逆时针方向排列的三角形面积为正，顶点按顺时针方向排列的三角形面积为负，故各个坐标分量 ， ， 都是可正可负的。

由定义可知，某个点M的面积坐标既可记为 ( ： ： )，也可记为 (k ：k ：k )（k≠0）。也就是说，一个点的面积坐标记法并非唯一，他们可以相差一个非0的常数因子，因此这类坐标属于齐次坐标，笛卡尔直角坐标不属于齐次坐标。3

当 + + =1时，面积坐标 ( ： ： )称为规范面积坐标。4

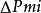三角形中任一点P与其3个角点相连形成3个子三角形，以原三角形边所对应的角码来命名此3个子三角形的面积，即 面积为 ， 面积为 ， 面积为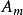 。P点的位置可有3个比值来确定，即

P( ， ， ）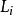

其中

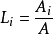
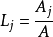
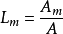
A是三角形的面积，因此有

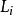+ + =1

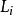称 ， ， 为面积坐标。

点的面积坐标符号设点M( ： ： )是规范面积坐标：

1）如果点M( ： ： )在三角形内部，那么 、 、 属于开区间 (0,1)；

2）如果一点在三角形的边上，至少有一个面积坐标 为 0，其余分量位于闭区间 [0,1]；

3）如果有某个坐标小于 0，则位于三角形外部。

例 以a、b、c分别表示⊿ABC三角A、B、C所对的边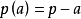，，，等等。

则⊿ABC的“五心”的面积坐标如下：5

重心：；

内心：（ ： ： ）；

旁心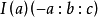：，余类推；

垂心：；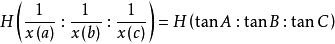

外心：。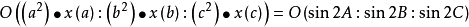

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学