[科普中国]-积分几何学

积分几何学是通过各种积分考察图形性质的一门学科，本质上属于整体微分几何范畴。积分几何的研究从欧氏平面和三维欧氏空间开始，逐步拓广到高维欧氏和非欧空间，然后概括到满足一定条件的齐性空间。

简介积分几何学是通过积分研究图形性质的一门学科。本质上属于整体微分几何的范畴。它起源于几何概率的研究，其发展也始终与几何概率相联系。积分几何的研究从二维欧几里得平面、三维欧几里得空间开始，逐步拓广到高维欧几里得空间和非欧几里得空间，然后概括为满足一定条件的齐性空间。积分几何的基本概念就是对于某种几何元素集定义一种在某种变换群作用下不变的密度和测度。该不变密度的不同表达式往往是导出重要结论的基础。

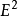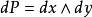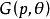基本信息以二维欧几里得平面 为例，设(x,y) 是平面上点P 的直角坐标，则在运动群作用下不变的点密度是 。设 表示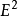 上的直线，它的方程是 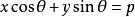，其中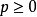 是坐标原点到直线的距离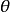， 是从原点 O 到直线的垂线与横坐标轴所成的有向角 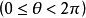则直线的密度是 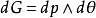。若它与平面上长度为 L 的曲线 C 的交点数为 则有著名的克罗夫顿公式(Crofton formula)

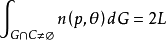
在 E2上，设图形 F 在作刚体运动，在 F 上固联一个正交标架R。假设对于平面上一个固定的正交标架R0而言，R的原点坐标为(x,y),且R 的第一条轴与R0 的第一条轴间的夹角为 θ,则定义F 的不变运动密度为 设E2 上有长度为Li 的曲线Ci= 1,2。让曲线C1固定，曲线C2 作刚体运动，其运动密度记为dC2,并设 C2 在任意位置与 C1 的交点数均有限，记为 n，则得庞加莱公式(Poincareformula)

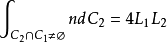
再设Ci 是分段光滑的简单闭曲线，其全曲率为ci(即Ci的各段光滑曲线的相对曲率关于弧长参数的积分之和，再加上各角点处的外角)，所围的区域记为Di其面积为Si，用 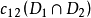表示相交区域 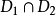的边界的全曲率。让曲线C1 固定，曲线 C2作刚体运动，把c12 对所有可能的 C2的位置进行积分，则有布拉施克运动公式(Blaschke's kinematic formula)

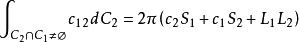设χ 为交集 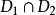的连通分支数，则上面的公式成为

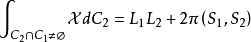所有上面的结果都可以推广到高维空间。1

发展简史几何概率的研究要以有关的图形集合的测度为基础，因而自然要导致积分几何的建立。一般认为,最早的几何概率问题是 G.-L.L.de布丰提出并解决的投针问题：设在平面上有一组平行线,其行距都等于D；把一根长度l