[科普中国]-离散量

离散量有两个含义，它可以指与连续量相对的、是指分散开来的、不存在中间值的量；也可以指描述数据离散趋势的统计量，常用的表示数据离散趋势的统计指标有全距、四分位区间距、平均差、方差和标准差。

与连续量对应的离散量基本介绍可以说“这个筐里有多少个苹果”，而不能说“这个桶里有多少个水”，对于水只能说多少而不能说多少个。这样，多少个和多少之间就有了明显的区别。

苹果是一个个分离、独立存在的，像这类东西(数学上称作集)在数数目的时候，回答是多少个，这类东西就称作离散量。例如，人群、鸟群、棍子捆，全都是离散量，因为这些都是一个个相互分离的。在数离散量时总是说1，2，3，…，称为自然数或正整数。

与数多少个的离散量相比较，像测量水有多少这样的量就称作连续量。因为桶里的水不是一个个分离的，而是连续变化的。

水无论分到多么细小也是水，是不会变的。还有，当把两个桶里的水倒在一起，仍然是连续的水，看不到有接缝的地方。

像这样能够自由地分开和结合的东西就称为连续量。然而，离散量和连续量的区别也并不是绝对的。例如，我们说多少米的布料是连续量，但若将其缝制成人们所穿的西装，就必须考虑它已成为离散量了。另外，俄国有一个故事说；“有位老奶奶要给三个孙子分吃两个土豆，因为不好分割，就把土豆做成了汤，分给三个孙子喝了。”老奶奶是把离散量的土豆，变成了连续量的土豆汤，从而解决了难题。在人类靠摘取树木的果实和猎取野兽来维持生活的时候，只数离散量就足够了，不会产生什么差错。在数树木的果实和野兽这样的离散量时，就说1，2，3，…自然数就行了。后来随着农业和畜牧业的发展，集体活动和集体生活的兴盛，就有了考虑连续量的要求了。假定有10个人捕获了7只鹿，当需要把7只鹿的肉分成相等的10份的时候，或者需要用鹿肉去交换其他东西的时候，自然就产生了考虑分割连续量的问题了。另外，像谷物的量、田地的面积、道路的里程等都是需要知道的，而这些都是连续量1。

物理学中的连续量和离散量连续量通常称做模拟量，它在时间上和数量上是连续的物理量。如温度计用水银长度来表示温度高低。其特点是数值由连续量表示，其运算过程也是连续的。温度变化的连续量曲线图如图1所示。

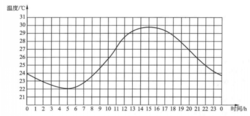
离散量又称数字量，它是将模拟量离散化之后得到的物理量。即任何仪器设备对于模拟量都不可能有完全精确的表示，因为它们都有一个采样周期，在该采样周期内，其物理量的数值都是不变的，而实际上的模拟量则是变化的。这样就将模拟量离散化，从而成为离散量。如一天中以每小时为单位测量一次温度的值，则得到24h内离散的时间点上的温度值，如图2所示2。

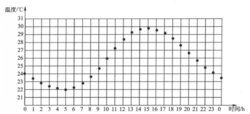
描述离散趋势的统计量尽管集中量可以很好地描述一组数据的特征，但仅用这些统计量还是不够的。还需要考虑数据的分散情况。有时，两组数据的平均数和中位数可能完全相同，但这两组数据之间会存在着很大的区别。请看下面两组数据：

A组：79 79 79 80 81 81 81

B组：50 60 70 80 90 100 100

这两组数据的平均数和中位数均为80，但不能据此就简单认为这两组学生的水平是一样的。A组数据与B组数据之间显然是有区别的。首先，A组中的数据相对比较集中，每个数据的值与平均数80相差无几；而B组中的数据相对分散一些，参差不齐，它反映了数据分布的另一个重要特征——变异性(variability)。描述数据离散趋势的统计量称为离散量(measures of dispersion)，或称差异量。

集中量描述了一组数据的典型情况，离散量则反映了数据的特殊情况。在研究一组数据的特征时，不但要了解其典型情况，而且还要了解其特殊情况，前面的例子中A组数据和B组数据的集中量相同，但其离散量肯定是不同的，只有同时了解了这两组数据的集中量和离散量，才能更为透彻地了解这两组数据之间的差别。常用的表示数据离散趋势的统计指标有全距、四分位区间距、平均差、方差和标准差3。

全距全距是说明数据离散程度的最简单的统计量。把一组数据按从小到大的顺序排列，用最高分减去最低分，所得的值就是全距，即最高分和最低分之问的距离。上面A组数据的全距为 ；B组数据的全距为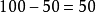 。全距小，说明数据的分布相对集中；全距大，说明数据的分布较为分散。全距的优点是计算方法简单，而且也容易理解。缺点是由于它只考虑到两端的数值，没有考虑中间数值的差异情况，描述数据时不太稳定。

四分位区间距中位数可以用来表示一组数据分布的集中趋势。中位数正好把一组数据一分为二。如果把中位数左侧和右侧的分布再各分成两个部分，得到的是四个相等的分位。这组数据的第一个四分位(即25%的位置)的值正好处于数据分布的四分之一处，中位数正好是第二个四分位的值，第三个四分位的值刚好位于该组数据分布的四分之三处。把第三个四分位的值减去第一个四分位的值，所得到的值叫做四分位区间距(inter-quartile range，IQR)，统计学上也用这种方法来表示数据的离散情况。如上面A组数据的四分位区间距为 ；B组数据的四分位区间距为 。除了四分位区间距，统计学上还有十分位区间距和百分位区间距，它们的区分方法相同，十分位则将数据由大到小或由小到大排序后，用9个点将全部数据分为十等份，与9个点位置上相对应的变量称为十分位数(deciles)，分别记为 ，表示10%的数据落在D1下，20%的数据落在D2下……100%的数据落在D9下。百分位区间距与十分位区间距同例，只是将数据分成100等份，于99个分割点位置上相对应的变量称为百分位数(Percentiles)，分别记为P1，P2，…，P99，表示1%的数据落在P1下……99%的数据落在P99下3。

平均差与全距相比，四分位区间距在表述数据的离散情况时稍微好一些，但由于它没有把所有的数据都考虑在内，其稳定性会差一些。比如说，我们得到两组数据，这两组数据的值并不完全一样，但最后得到的四分位区间距的值则可能完全一致，这便是用四分位区问距来表示数据分布的不足之处。理想的办法是把全部数据都考虑在内来计算分布程度。理由很简单：平均数代表一组数据的集中趋势，我们把一组数据中的每个数据与平均数相比较就可以得知每个数据与平均数偏离的程度，或者说与平均数差异的情况。如果把这组数据中每个数据与平均数差异的情况相加起来，那么所有数据的差异情况便一目了然。把这个值除以数据的个数，所得的值叫做平均差。其计算公式为：

平均差=

其中，=每个数据的值；

=总体平均数；

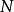=观测的数据个数。

从上式可知，平均差是数据分布中所有原始数据与平均数距离的绝对值的平均。用绝对值是为了不出现负数。由于平均差是根据分布中每一个观测值计算求得的，它较好地代表了数据分布的离散程度。然而，由于平均差的计算要求绝对值，不利于进一步的统计分析，故在统计实践中平均差不常使用。

方差与标准差根据上面的公式，如果不求每个原始数据与平均数之差的绝对

平均值，而是求它们之间的平方，这样就不会有负数出现了。然后再把每个原始数据与平均数之差的平方的值加起来，得到的是每个原始数据与平均数之差的平方和：。用这个平方和再除以所观测到的数据的个数，得到的值被称作方差。用公式表示为：

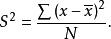
由于方差的值相对来说比较大，一般情况下人们使用标准差来代表数据的离散程度。标准差就是方差的平方根，其计算公式为：

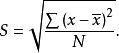
标准差与方差的概念易于理解，它们实际上都是一个差异量数：标准差的平方就是方差，或方差的平方根就等于标准差，二者都反映了一组数据围绕平均数分布的情况。标准差的值越大，表明这组数据的离散程度也越大，即数据越参差不齐，分布范围越广；标准差的值越小，表明这组数据的离散程度越小，即数据越集中、整齐，分布范围越小。当数据完全没有差异时，所有数值都与平均数相等，这时标准差或方差等于零。

有一点需要说明：在上述公式中我们用N作为除数，所得结果并不是十分准确的。这是因为在一般情况下，总体参数是未知的，只能用样本统计量作估计值，譬如用样本标准差(S)作为总体标准差()的估计值。可以证明，在公式中用N作为除数时(尤其是当N很小时)，所得出的作为总体标准差估计值的样本标准差是有偏差的，而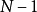作除数时，所得标准差则是无偏差的。因此，比较稳妥的做法是用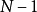作除数。当然，当N比较大时，用N或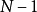作除数，所得结果差别不大3。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学