[科普中国]-分支过程

分支过程，是一种特殊的随机过程，它是一组粒子的分裂或灭亡过程的数学模型。

定义分支过程是一种描述群体中个体数量的时齐马尔可夫链。

离散时间分支过程设 表示群体的第 n 代的个体总数，如果假定群体中每个个体之“子女”个数是独立同分步的随机变量，则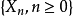 为[离散时间] 分支过程。以 表示第 n 代中第 k 个个体的“子女”个数，于是

由假设知诸相互独立，并且与整值随机变量 Y 有相同的分布。

假定 Y 的母函数为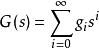。可以证明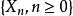 是时齐的马尔可夫链，在 的假设下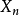， 的母函数为

其中 为 的 n 重复合。

于是此链的转移阵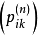（从而有穷维分布）由完全确定。如果群体中的个体数不能按“代”计算，而只能以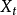 表示时刻 t 代个体总数，这时可考虑连续时间分支过程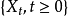。1

连续时间分支过程设时间参数 t≥0 连续，b(t)Δt 表示在短时间 (t,t+Δt) 中发生一次分裂的概率，pk(t) 表示一个粒子分裂为 k 个的概率(k=0,1,2,…)。若 b(t) 、 pk(t) 连续，b(t)>0,则在时刻 t 的粒子数 Z(t) 构成一连续时间马尔可夫链，于是可利用后者的理论来研究 {Z(t)} 。若 b(t)，pk(t) 不依赖于 t ，则 {Z(t)} 是齐次的马尔可夫链，这时可以得到许多类似于对 G-W 过程所得到的结果。23

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学