[科普中国]-简单相关

简单相关是两类变量之间线性或非线性的不确定的关联关系，又称二元相关、单相关。在简单相关情形下，两个变量之间相关关系，可能是正相关的或负相关的，或者是无相关的。无相关，亦称零相关或完全不相关，其相反情形是完全相关。

基本介绍统计相关关系按相关因素的多少分类可分为简****单相关和复相关。

****简单相关(simple correlation)也称单相关，是指两个变量之间的相关方向和程度的分析。例如，家庭收入水平和食品支出比重之间的相关关系分析。

复相关(multiple correlation)指两个以上的变量之间的相关分析。例如，商品购买力与居民货币收入、居民非商品支出、手存现金、储蓄等因素之间的相关关系分析等1。

相关关系的判断面对杂乱的社会经济现象，人们常将其观察的结果数量化为统计数据，并初步判断其间的相关关系。这种判断一般是根据理论或经验借助相关表、相关图等工具进行的，并在此基础上需要做关系密切程度的测定。

理论与经验分析这是对相关事物的关系最为关键的分析，如果现象之间的关联已被前人发现，我们就要参照其总结的规律和经验，对其进行量化的证实或证伪。如果现象之间确实存在着未被人们认知的客观联系，在数量化的统计资料中必然要显现出来。经过我们的研究可以总结或升华为经济理论。

在理论分析中有些现象之间看似密切相关，但其未必具有直接的必然联系。如彩色电视机与电冰箱的销售量，两者在一段时间内同时增长，看起来密切相关，能说这两种现象具有客观的必然联系吗? 显然不能。其实，它们都受购买力水平的制约。在购买力水平较高且大幅度增长的条件下，这两种商品的销售量才可能同时增长。如果购买力水平较低且增长有限，可能其中的一种商品的销售量增长，另一种商品的销售量稳定甚至下降；或者一种商品的销售量增长快，另一种商品的销售量出现波动状态。

可见，理论分析是测定相关关系的前提。由于现象之间的相关关系比较复杂，测定相关关系之前，除了理论分析以外，还要利用相关表和相关图粗略地判断现象之间的相关程度和相关形态1。

相关表和相关图相关表(correlation table)是反映现象间关系的数据表格，常有简单表与复杂表之分：一般的简单相关表是将具有相关关系的两个变量值按其中一个的大小顺序排列，另一个依其对应关系编排而成的统计表。它是粗略观察现象之间相关程度的一种有效工具，同时也是绘制相关图和测定相关关系的依据。复杂表是以一个变量顺序排列为行标目，而另一个变量的顺序排列为列标目，所有的统计数据都在各行和列的交义点上，这样数据的分布就反映出了相关的大致程度和方向了。

相关图(correlation graph)也称相关散点图，它是将具有相关关系的两个变量值描绘在坐标图上。以横轴表示变量X(常为自变量)，纵轴表示变量Y(常为因变量)，按两变量的对应值标出坐标点的分布状况的统计图。它是粗略观察现象之间相关程度和相关形态的一种有效工具，它为测定相关关系奠定有效基础。如表1所示。

|| || 表1 相关图

相关表和相关图均具有粗略观察现象之间相关关系的功能；相关图与相关表相比较，还有观察相关形态的作用；但相关图必须以相关表提供的资料为依据来绘制1。

相关程度的测定测定线性相关的密切程度的常用方法是皮尔逊相关系数，现就其主要内容介绍如下:

相关系数的含义相关系数(correlation coefficient)是皮尔逊相关系数的简称，有时也叫简单相关系数。它是在线性相关的条件下，说明两个现象之间紧密程度的统计分析指标。

它具有四个特点:

(1) 两变量为对称关系(或称“对等关系”)，即可以不区分自变量和因变量；

(2) 相关系数只有一个值，不受自变量和因变量换位的影响；

(3) 相关系数有正负号，反映正相关或负相关；

(4) 若以抽样调查取得资料，则两变量均应有相同的随机性，这也是对称关系的要求。对全面统计资料而言，不存在随机性的问题，均为确定性资料。

相关系数的计算方法有若干种，最易理解的一种叫积差法，直接来源于数理统计中相关系数的定义。相关系数的定义(积差法)为：两变量的协方差与两变量各自标准差乘积之比。其相应的定义公式为：

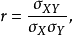式中，代表相关系数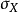；为变量X的标准差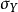；代表变量Y的标准差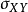；代表变量X与Y的协方差。对相关系数进行等价变换，可以得到很多表达式，如：

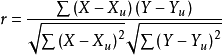
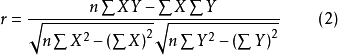
表示变量X和Y的线性相关方向和相关程度，取值范围为。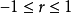

当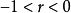时，相关图分布呈现出Y随X的增加而减少的负斜率趋势，即为负相关；当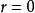时，相关图分布通常呈现出不规则状态，变量Y不受变量X的影响，表明X和Y之间没有线性相关关系。但必须注意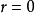，，只能说明X与Y之间没有线性相关关系，而不能随意排斥其它相关关系，或许存在着某种形态的曲线相关。

当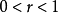时，相关图分布呈现出Y随X 的增加而增加的正斜率趋势，即为正相关。

当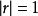时，相关散点图呈现在一条直线上，即Y与X完全线性相关。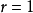,时，表现为完全正相关；时，表现为完全负相关。

为了判断现象之间相关程度的高低，人们根据经验一般将社会经济现象中的相关系数划分为四个等级: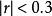为不相关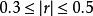，为低度相关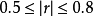，,为显著相关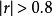，为高度相关。

相关系数的计算(1)根据定义或公式先计算式中的各要素，然后用来计算求得相关系数。

(2)利用统计软件进行计算。使用任何一款统计软件，都可以直接计算相关系数。

相关系数的检验由于我们在现实的统计中往往只能得到一个样本，所以根据样本计算的相关系数就具有一定的随机性，即与总体相关系数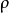之间有一定的差别。这就需要采用假设检验的方法对样本相关系数的显著性做出判断。经英国统计学家费雪做如下变换：

和

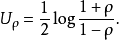这里的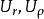都接近服从正态分布，因此可以利用样本相关系数估计总体相关系数。即在原假设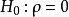成立时，具有如下检验统计量：

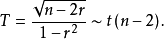即当时，否定原假设1。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学