复合函数是按一定次序把有限个函数合成得到的函数,对两个函数f:A→B,g:B→C,由h(x)=g(f(x))(x∈A)确定的函数h称为f与g的复合函数,记为g°f,这样,g°f是A到C的函数,(g°f)(x)=g(f(x)),它的值域是g(f(A)),记号“°”表示两个函数的复合,它是二元运算.这个运算不满足交换律,即一般来说g°f≠f°g,但它满足结合律:对f:A→B,g:B→C,h:C→D,有h°(g°f)=(h°g)°f,于是可以定义h°g°f=h°(g°f)=(h°g)°f,一般地,对n+1个满足Bi⊆Ai+1(i=1,2,…,n)的函数fi:Ai→Bi(i=1,2,…,n+1)可以定义n重复合函数fn+1°fn°…°f1,任给两个函数f:A→B,g:C→D,当且仅当f(A)⊆C时可以得到复合函数g°f:A→D;当且仅当g(C)⊆A时可以得到f°g:C→B,当函数用变量表示为t=f(x),y=g(t),且f的值域含于g的定义域时,称t为复合函数y=g(f(x))的中间变量,函数的复合是研究函数的一种工具,一方面它提供了构造各式各样的新函数的方法;另一方面,为研究复杂的函数,常将它们看成一些简单函数的复合(求函数的导数时常这样做)1。
定义设有定义在由集合A到集合B的函数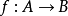 和定义在集合B到集合C上的函数
和定义在集合B到集合C上的函数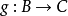 ,则
,则 和
和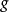 的复合函数是一个由集合A到集合C的函数,记为
的复合函数是一个由集合A到集合C的函数,记为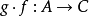 (或记为
(或记为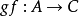 )。
)。
对于任意一个元素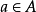 ,有
,有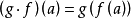 ,也就是说,如果
,也就是说,如果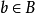 是
是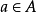 在函数
在函数 作用下的像,并且
作用下的像,并且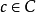 是元素b在函数
是元素b在函数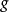 作用下的像,那么集合C中的元素c就是
作用下的像,那么集合C中的元素c就是 在复合函数
在复合函数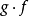 作用下的像2。
作用下的像2。
复合函数的定义域与值域在上述复合函数的定义中,要求函数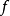 的值域包与函数g的定义域相等。实际上,对该条件可以适当放宽,即只要求函数
的值域包与函数g的定义域相等。实际上,对该条件可以适当放宽,即只要求函数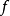 的值域
的值域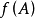 是函数g的定义域的子集就可以了。也就是说.若有函数
是函数g的定义域的子集就可以了。也就是说.若有函数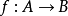 和函数
和函数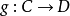 ,并且有f(A)是集合C的子集,则同样可以定义一个由集合A到集合D的复合函数g·f。但是,如果
,并且有f(A)是集合C的子集,则同样可以定义一个由集合A到集合D的复合函数g·f。但是,如果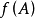 不是集合C的子集,那么,复合函数
不是集合C的子集,那么,复合函数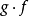 就没有意义了。因此,在上述定义的条件下,尽管复合函数
就没有意义了。因此,在上述定义的条件下,尽管复合函数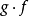 有意义,但是
有意义,但是 不一定有意义,即使
不一定有意义,即使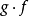 与
与 都有意义,二者也不一定相等。
都有意义,二者也不一定相等。
例1 设集合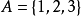 ,集合
,集合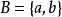 ,集合
,集合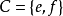 ,定义在集合A到集合B上的函数
,定义在集合A到集合B上的函数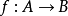 ,
,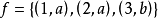 ,定义在集合B到集合C上的函数
,定义在集合B到集合C上的函数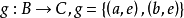 ,求复合函数
,求复合函数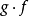 。
。
根据复合函数的定义不难求出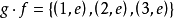
例2设集合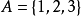 ,并且在由集合A到A自身上定义两个函数
,并且在由集合A到A自身上定义两个函数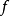 和函数
和函数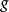 :
:
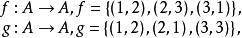 求复合函数
求复合函数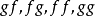 。
。
**解:**根据复合函数的定义有:
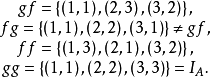 由于函数的复合运算是关系的复合运算的一种特殊情形,因此关系的复合运算中成立的性质,对于函数的复合运算也是成立的。例如,对于任意一个函数
由于函数的复合运算是关系的复合运算的一种特殊情形,因此关系的复合运算中成立的性质,对于函数的复合运算也是成立的。例如,对于任意一个函数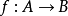 ,有
,有 。又例如,设有三个函数
。又例如,设有三个函数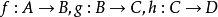 ,根据定义不难看出,这些函数可以构成复合函数
,根据定义不难看出,这些函数可以构成复合函数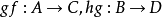 ,进而可以构成复合函数
,进而可以构成复合函数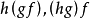 ,可以看出,这两个复合函数都是由集合A到集合D的函数。又由于关系的复合运算满足结合律,因此,函数的复合运算也满足结合律,因此,可以得出以下定理2。
,可以看出,这两个复合函数都是由集合A到集合D的函数。又由于关系的复合运算满足结合律,因此,函数的复合运算也满足结合律,因此,可以得出以下定理2。
相关定理定理1 设对于任意给定的三个函数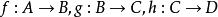 ,则有
,则有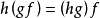 。
。
定义 设有定义在集合A到A自身的函数 ,且
,且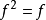 ,则称函数
,则称函数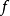 为幂等函数。例如,定义在正整数集的幂集上的函数
为幂等函数。例如,定义在正整数集的幂集上的函数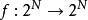 ,将其定义为
,将其定义为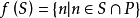 ,则根据函数
,则根据函数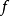 的定义,对于任意一个
的定义,对于任意一个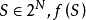 为S中所有的素数组成的集合,记为
为S中所有的素数组成的集合,记为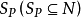 。而又由于
。而又由于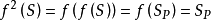 ,所以
,所以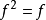 ,因此这里定义的函数
,因此这里定义的函数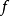 是一个幂等函数。
是一个幂等函数。
如果函数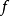 是幂等函数,那么对于所有的正整数n≥1,都有
是幂等函数,那么对于所有的正整数n≥1,都有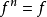 。
。
定理 设有函数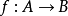 和函数
和函数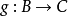 ,那么:
,那么:
(1) 如果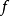 和
和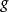 都是单射函数,则复合函数
都是单射函数,则复合函数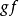 也是单射函数;
也是单射函数;
(2) 如果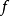 和
和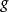 都是满射函数,则复合函数
都是满射函数,则复合函数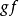 也是满射函数;
也是满射函数;
(3) 如果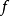 和
和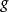 都是双射函数,则复合函数
都是双射函数,则复合函数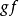 也是双射函数。
也是双射函数。
定理 设有函数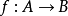 和函数
和函数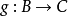 ,那么:
,那么:
(1) 如果复合函数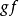 是单射函数,则函数
是单射函数,则函数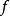 是单射函数;
是单射函数;
(2) 如果复合函数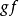 是满射函数,则函数g是满射函数;
是满射函数,则函数g是满射函数;
(3) 如果复合函数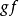 是双射函数,则函数
是双射函数,则函数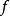 是双射函数,函数g是满射函数2。
是双射函数,函数g是满射函数2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国