[科普中国]-埃及数字

古埃及人的数字体系是十进制的，人们把数字以图画的形式把数字刻下或者写下来，而不是以文字的形式。单位数字由一条竖线表示，而10的幂次，从10、100、1 000、10 000、1 00 000到1 000 000，古埃及人用不同的符号表示，1 000 000也被记作“我数不清的数字”。古埃及人把倍数完整的写下来而不是用缩写，比如9写成9条竖线，350写成3个100和5个10。古埃及人没有表示零的符号1。

基本介绍古埃及数字(ancient Egyptian numerals)是古代人类最重要、最基本的数字之一。指古埃及人创造的一种十进制象形文数字。约公元前4000年，埃及就已有了相当发达的文化，当时已有了象形文字，现在尚存于英国牛津博物馆的埃及王室的权标；存于莫斯科国立普希金造型艺术博物馆里的莫斯科数学纸草书；存于英国博物馆的莱因德纸草书；存于法国卢佛尔博物馆的罗林纸草书(尼罗河三角洲上生长的一种形似芦苇的植物，把茎逐层撕开为薄片，古代用以著书，称纸草书)，上面都写有古埃及的象形文字，或另一种僧侣文字。象形文数字形如下图：

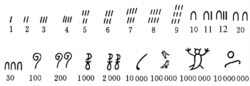
古埃及象形文数字用的是十进制记数法，由于没有位值制，所以数的记法比较麻烦，有多少个单位就要重复多少次，如24记为

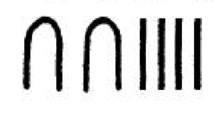
像986这个数，需要用23个符号来表示，除了象形文数字外，古埃及还有宗教文字，一般称为僧侣文，下面列出僧侣文的数字2。

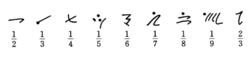
数字的名称及符号古埃及人将1~9个数字分别称为wa，senuj，khemet，jfedu，dju，sjsu，sefekhu，khemenu，pesedshu。古埃及人称10为medshu，并且用形如“轭”的符号来表示；称100为shenet，用一圈绳子表示；称1 000为kha，用一枚莲花表示；称10 000为dsheba，用一个指头表示；称100 000为hefen，用一只蝌蚪表示；称1 000 000为heh，用举着两条胳膊端坐着的神来表示。记载日期和计数时所用的序数通过在基数后面加后缀-nu或者前面加前缀mech-来表示1。

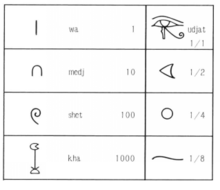
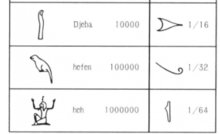
相关介绍大约在公元前3100年左右， 埃及人沿尼罗河两岸建立了统一的国家，与此同时发明了象形文字。在一根当时的王室权标上，用象形文字记载着几个以百万和十万计的大数。尼罗河的定期泛滥，使人们每年都要重新丈量耕地面积。从公元前2900年左右开始， 埃及人建造了许多巨大的金字塔，其测量精度是惊人的。因此，埃及人很早就有了丰富的算术与几何知识。根据大约公元前1850—前1650年间的两份纸草书 (参见“莫斯科纸草书”、“阿默斯纸草书”)人们进一步了解到埃及古代数学的丰富内容3。

埃及人建立了以10为基数的数字符号。由于完全没有位值的概念，他们需要为10的每一幂次设计一个新的符号，这些符号大致如下：

一般数字是将10的各个幂次按加法原则累积而成，这使得数的表示与各种运算都十分烦琐。大约在中王国时期(约公元前2133—前1786)。由象形文字演变出一种僧侣文字，在写法上简化了许多，前面提到的两种纸草书就是用这种文字写成的， 其中的数字符号写法是：

埃及人掌握了完整而正确的加减乘除运算方法。由于数字记法的累加性， 加减法可以直接通过添加或去掉一些符号而完成。乘法相当烦琐。他们发明了形如1/n(n是自然数)的单位分数。一般分数均表示为单位分数的和，为此编制了专门的分解表。除法是根据乘法的逆运算原理或利用分数分解表实现的。

埃及人解决了一些在今天看来属于代数学范围的问题。他们的 “堆算”常被认为是一元一次方程。约公元前1950年的卡洪Kahun纸草书中的一个问题则被认为是二次方程，原题是：“把一个面积为100的正方形分为两个较小的正方形， 使其中个的边长是另一个的3/4”。还有的问题涉及等差与等比数列中的几项。但是，所有这些问题都是用加、减、乘、除、比例等典型的算术方法求解的，至多涉及开平方运算，其典型方法是基于比例原理的试位法(参见该条)， 很难说其中已经包含了代数学的思想与方法。

埃及人有着丰富的几何知识， 他们正确地计算了正方形、长方形、直角三角形，等腰三角形、直角或等腰梯形，以及可以分解为这些图形的田地面积，他们的圆面积(参见该条)公式相当于圆周率取3. 16049，这在当时是了不起的成就。他们也正确地计算了立方体、长方体、棱柱、圆柱的体积，特别是以对称的形式给出了正四棱台的体积公式(参见“莫斯科纸草书”)，他们的圆台、半球体积公式却是相当粗糙的。

埃及古代数学基本上仍然是一门实用技术。其结果仍然是经验性的， 但这些内容对于后世数学的发展又是必不可少的， 辉煌的希腊古代数学正是在继承了巴比伦与埃及的丰富遗产之后发展起来的3。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学