p级数,又称超调和级数,是指数学中一种特殊的正项级数。当p=1时,p级数退化为调和级数。p级数是重要的正项级数,它能用来判断其它正项级数敛散性。
定义定义. 对任意的正实数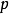 ,称下列级数1
,称下列级数1
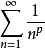 为
为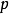 级数。显然,当
级数。显然,当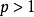 时,
时,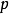 级数收敛,当
级数收敛,当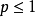 ,
,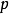 级数发散。当
级数发散。当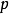 级数收敛时,记
级数收敛时,记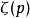 为
为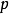 级数收敛值。易知
级数收敛值。易知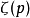 是
是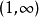 上的光滑函数1。
上的光滑函数1。
特殊值1)对任意的正偶数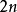 ,有
,有
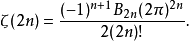
其中,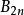 是第
是第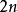 个伯努利数。对任意的正奇数,目前还没有这样的简单表达式。
个伯努利数。对任意的正奇数,目前还没有这样的简单表达式。
2)
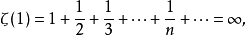
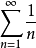 也称为调和级数,应此,由上式可知调和级数是发散的。
也称为调和级数,应此,由上式可知调和级数是发散的。
3)
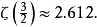
4)
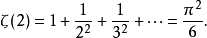
5)
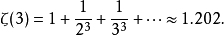
6)
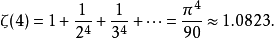
欧拉乘积公式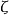 函数与素数之间有一重要的关系,即欧拉乘积公式,最早由数学家欧拉发现2。即为
函数与素数之间有一重要的关系,即欧拉乘积公式,最早由数学家欧拉发现2。即为
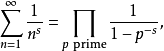 其中,表达式右边为
其中,表达式右边为
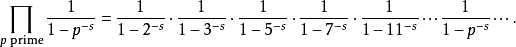 欧拉乘积公式表明
欧拉乘积公式表明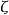 函数和素数之间有千丝万缕的联系。
函数和素数之间有千丝万缕的联系。
由欧拉乘积公式,我们有
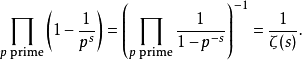
当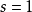 时,欧拉乘积公式左边为调和级数,是发散的,欧拉乘积公式右边为
时,欧拉乘积公式左边为调和级数,是发散的,欧拉乘积公式右边为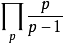 ,这表明素数是无穷多个。除此之外,上述公式还有很多其它用处。如欧拉乘积公式可用于计算随机选取的整数互质的渐近概率。
,这表明素数是无穷多个。除此之外,上述公式还有很多其它用处。如欧拉乘积公式可用于计算随机选取的整数互质的渐近概率。
黎曼函数定义. 在复平面上,对任意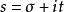 ,定义黎曼函数
,定义黎曼函数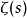 为
为
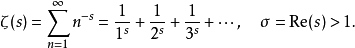 或者由下述积分给出
或者由下述积分给出
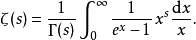 其中
其中
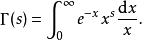
黎曼函数和黎曼猜想有关。而目前黎曼猜想是数学上还未解决的一个重要的猜想,其猜想是非平凡的零点的分布都位于复平面上 Re(s)=1/2 的直线上。进一步的了解参见黎曼猜想。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国