[科普中国]-电子迁移率

在电场下，力作用于自由电子，使电子朝电场的反向加速运动。根据牛顿第二定律，自由电子应当一直被加速，电流随时间持续增大。但我们知道电流到达一个定值后就不会增大，说明存在一个“摩擦力”反抗着电子的加速。摩擦力来自晶格缺陷对电子的散射，包括杂质原子、空隙、间隙原子、位错甚至原子自身的热振动。每个散射事件都使电子失去动能并改变运动方向。

在一定时间内，电子走过的路径不是其速率与时间的乘积，而是多次散射后走过的净长度。电压越高，散射越频繁；时间越长，散射事件越多；截面积越大，散射频率越低，故电子运动的净路径与电压和时间成反比。由此可定义出散射事件频率的物理量，称作电子迁移率μe。1

电子迁移率含义描述散射事件频率的物理量，称作电子迁移率μe，单位为[m2/（V·s）]。可以将材料的电导率σ表示为：

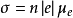
n为单位体积（m3）中自由电子数，〡e〡为电子电荷绝对值（1.6×1019C）。所以电导率与自由电子数和电子迁移率成正比关系。电子迁移率μe的物理意义为单位外电场作用下电子所获得的定向漂移速度。

能带理论指出，在具有严格周期性势场的理想晶体中的载流子，在绝对零度下的运动像理想气体分子在真空中的运动一样，不受阻力，迁移率为无限大。当周期性势场受到破坏，载流子的运动才受到阻力的作用，其原因是载流子在运动过程中受到了各种因素的散射。

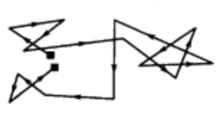
在有外加电场时，载流子在电场力的作用下作加速运动，漂移速度应该不断增加，电流密度将无限增大。但从欧姆定律可知，在恒定电场作用下，电流密度应该是恒定的。其原因是，在一定温度下，材料内部的大量载流子，即使没有电场作用，它们也不是静止不动，而是永不停息地作着无规则的、杂乱无章的运动，即热运动。同时晶格上的原子也在不停地围绕格点作热振动。对于半导体，其中还掺入一定的杂质，它们一般是电离了的，也带有电荷。载流子在材料中运动时，便会不断地与热振动着的晶格原子或电离了的杂质离子发生作用，或者说发生碰撞，碰撞后载流子速度的大小与方向发生改变。用波的概念，可以认为电子波在材料中传播时遭到了散射。载流子无规则的热运动也正是由于它们不断地遭到散射的结果。所谓自由载流子，实质上只在两次散射之间才真正是自由运动，其连续两次散射间自由运动的平均路程称为平均自由程，而平均时间称为平均自由时间。下图为载流子热运动示意图，在无外电场时，电子虽然永不停息地作热运动，但宏观上没有沿着一定方向流动，所以并不构成电流。

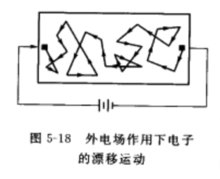
当有外加电场作用时，载流子存在着相互矛盾的两种运动。一方面，载流子受到电场力的作用，沿电场方向（空穴）或反电场方向（电子）定向运动；另一方面，载流子仍不断地遭到散射，使载流子的运动方向不断改变。这样，由于电场作用获得漂移速度，不断地散射到各个方向上去，使漂移速度不能无限地积累起来。载流子在电场力的作用下的加速运动，也只有在两次散射之间才存在，经过散射后，它们又失去了获得的附加速度。从而在外力和散射的双重影响下，使得载流子以一定的平均速度沿力的方向漂移，这个平均速度就是恒定的平均漂移速度。载流子在外电场作用下的运动轨迹实际上是热运动和漂移运动的叠加，见下图。因此在外电场的作用下，虽然载流子仍不断地遭到散射，但由于有外电场的作用，载流子会沿着电场方向或反方向有一定的漂移运动，形成电流，而且在恒定电场作用下，电流密度是恒定的。2

金属中的电子迁移率自由电子的运动可以在经典力学的基础上结合波粒二象性来讨论，这是因为它的量子化特征不很显著的缘故，例如它的能量就不是量子化的，而是可以连续变化。下面用经典力学理论讨论。

在外电场E作用下，金属中的自由电子可被加速，其加速度为:

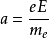
实际上导体都有电阻，因而电子不会无限地被加速，速度不会无限大。所以我们假定电子由于和声子、杂质、缺陷相碰撞而散射，从而失去前进方向上的速度分量。这就是金属有电阻的原因。发生碰撞瞬间，由于电子向四面八方散射，因而对大量电子平均而言，电子在前进方向上的平均迁移速度为0，然后又由于电场的作用，电子仍被电场加速，获得定向速度。设每两次碰撞之间的平均时间为2τ，则电子的平均速度为：

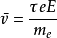
可求出自由电子迁移率：

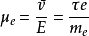
式中，e为电子电荷；me为电子质量；τ为松弛时间，则0.5τ为单位时间平均散射次数。τ与晶格缺陷及温度有关。温度越高，晶体缺陷越多，电子散射几率越大，τ越小。

以上是用经典力学模型来讨论自由电子的运动，实际晶体中的电子不是“自由”的。对于半导体和绝缘体中的电子能态，必须用量子力学理论来描述。使用量子力学理论描述的晶格场中电子迁移运动，可以得到电子迁移率μe为：

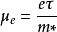
式中，e为电子电荷，m*为电子有效质量。3

影响电子迁移率的因素电子和空穴的有效质量的大小是由半导体材料的性质所决定的。所以不同的半导体材料，电子和空穴的有效质量也不同。平均自由运动时间的长短是由载流子的散射的强弱来决定的。散射越弱，τ越长，迁移率也就越高。掺杂浓度和温度对迁移率的影响，本质上是对载流子散射强弱的影响。散射主要有以下两方面的原因：

1.晶格散射

半导体晶体中规则排列的晶格，在其晶格点阵附近产生热振动，称为晶格振动。由于这种晶格振动引起的散射叫做晶格散射。温度越高，品格振动越强，对载流子的品格散射也将增强。在低掺杂半导体中，迁移率随温度升高而大幅度下降的原因就在于此。

2.电离杂质散射

杂质原子和晶格缺陷都可以对载流子产生一定的散射作用。但最重要的是由电离杂质产生的正负电中心对载流子有吸引或排斥作用，当载流子经过带电中心附近，就会发生散射作用。如下图所示。

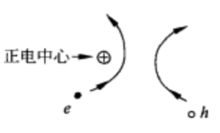
电离杂质散射的影响与掺杂浓度有关。掺杂越多，教流子和电离杂质相遇而被散射的机会也就越多。

电离杂质散射的强弱也和温度有关。温度越高，载流子运动速度越大，因而对于同样的吸引和排斥作用所受影响相对就越小，散射作用越弱。这和晶格散射情况是相反的，所以在高掺杂时，由于电离杂质散射随温度变化的趋势与晶格散射相反，因此迁移率随温度变化较小。3

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所