[科普中国]-剩余误差

剩余误差（residual errors）是各次测量值与其算术平均值之差，也称残差、残余误差。在等精度测量中，x为算术平均值；在不等精度测量中，x为加权平均值。 可以证明残差的代数和等于零和残差的平方和为最小值。 这两点特性是检验算术平均值是否正确的依据，也是建立最小二乘法的理论依据。残差在误差理论中是一个经常遇到的重要参数。

随机误差的特征一般就随机误差的个体而言，其大小和方向都无法预测，而就随机误差的总体而言，则具有统计规律性，服从某种概率分布。大量实验证明，随机误差服从以下统计特征：

(1)绝对值相等的正误差与负误差出现的次数相等，称为随机误差的对称性；

(2)绝对值小的误差比绝对值大的误差出现的次数多，称为随机误差的单峰性；

(3)在一定的测量条件下，随机误差的绝对值不会超过一定界限，称为随机误差的有界性；

(4)当测量次数增加，随机误差的代数和趋向于零，称为随机误差的抵偿性1。

随机误差的概率分布随机误差的概率分布有正态分布、均匀分布、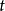分布、反正弦分布、梯形分布、三角分布等。绝大多数随机误差服从正态分布，因此，正态分布规律占有重要地位。

正态分布的随机误差，其概率密度函数为

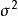式中 和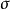——随机误差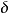的方差和标准差，标准差定义为方差的正的算术平方根；

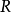被测量的真值；

m——测量值。

如果确定了R及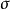，则正态分布曲线就可以确定。现在需要解决的是在已知一组被测量后如何估算R及。

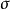算术平均值和剩余误差首先，在不考虑系统误差和粗大误差的条件下，对被测量作多次测量，由于各种随机因素的影响，即便在同样条件下，各次测量值均有一定的差异。设测量序列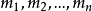，则用绝对误差表示的随机误差列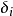为

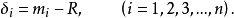将上式两边求和得

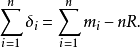或

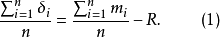由正态分布的抵偿特性，得

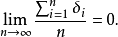故由式(1)得

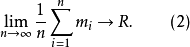式(2)左边即为随机变量的数学期望，当n为有限值时，测量值序列的算术平均值为

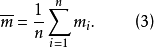式中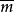：为测量值序列的算术平均值。

式(2)和式(3)表明，无系统误差存在时，当测量次数n无限增大时，测量值的算术平均值与真值无限接近。因此可以说，在等精度测量中，算术平均值是被测量最可信赖的值。

由此可见，如果能够对某一被测量进行无限次测量，就可以得到不受随机误差影响的测量结果，或者影响很小，可以忽略不计。但由于实际测量都是有限次测量，处理时只能把算术平均值作为被测量的真值的最佳近似值，于是有剩余误差（残余误差）表达式：

式中 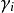为剩余误差1。

剩余误差的性质剩余误差有两个性质：

剩余误差的代数和为零，即

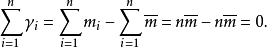利用剩余误差的这一性质，可以检验计算的剩余误差和算术平均值是否准确。

剩余误差的平方和为最小，即

这是最小二乘法原理，在试验数据处理中常常用到1。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学