[科普中国]-绝对偏差

绝对偏差(absolute deviation)指个别测定值与多次测定平均值之差，简称偏差。数学表达式为：绝对偏差=个别测定值-多次测定的算术平均值。

基本介绍当我们进行任一测量时，由于测量设备、测量方法、测量环境、人的观察力和被测对象等，都不能做到完美无缺，而使测量结果受到歪曲，表现为测量结果与待测量真值间存在一定差值，这个差值就是测量误差1。

由此可知，误差是不能完全消除的，只能减小和削弱，这也正是我们研究误差理论的主要目的。

表示误差的常用方法有以下几种：

(1)绝对误差和相对误差；

(2)绝对偏差和相对偏差；

(3)平均偏差和相对平均偏差；

(4)极差；

(5)样本的差方和、方差、标准偏差和相对标准偏差。

绝对误差是测量值(单一测量值或多次测量值的均值)与真值之差。测量结果大于真值时，误差为正，反之为负。

相对误差为绝对误差与真值的比值(常以百分数表示)。

绝对偏差为某一测量值与多次测量值的均值之差。

相对偏差为绝对偏差与均值的比值(常以百分数表示)。2

极差为一组测量值中最大值与最小值之差。又称范围误差或全距，以R表示，即。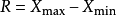

相关概念平均偏差指各次测量值的绝对偏差绝对值的平均值。

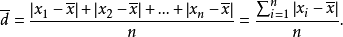
相对平均偏差指平均偏差占平均值的百分率。

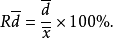
标准偏差指多次平行测定值(测定次数或样本数n≤20)偏离平均值的距离的平均数，它是方差的算术平方根，其计算公式如下：

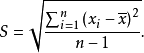式中，n-1为样本自由度。当n趋向无穷大时，n-1趋向n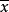，趋向等于真实值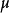。此时的标准偏差称为

总体标准偏差，符号为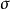，其计算公式如下：

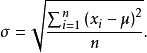
相对标准偏差指标准偏差占平均值的百分率，又称为变异系数(CV)，通常用RSD表示2。

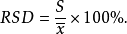
差方和样本差方和：

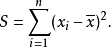
方差样本方差：

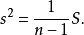
平均绝对离差平均绝对离差(mean absolute deviation)是用样本数据相对于其平均值的绝对距离来度量数据的离散程度。平均绝对离差也称为平均离差(mean deviation)。平均绝对离差定义为各数据与平均值的离差的绝对值的平均数。

设样本的n个观测值为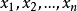，平均绝对离差为：

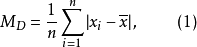
对于分组数据，平均绝对离差为：

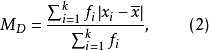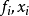其中分别为第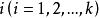组数据的频数及组中值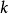，为数据分组的组数。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学