对于n次多项式F(X)有著名的牛顿恒等式。它是n次方程F(X)=0的n个根的同次幂的和与F(X)的函数之间关系的明确表述1。
背景艾萨克·牛顿(Isaac Newton)是英国伟大的数学家、物理学家、天文学家和自然哲学家,其研究领域包括了物理学、数学、天文学、神学、自然哲学和炼金术。
牛顿的主要贡献有发明了微积分,发现了万有引力定律和经典力学,设计并实际制造了第一架反射式望远镜等等,被誉为人类历史上最伟大,最有影响力的科学家。为了纪念牛顿在经典力学方面的杰出成就,“牛顿”后来成为衡量力的大小的物理单位。数学方面牛顿也贡献颇多,以他和莱布尼兹共同发明的微积分最为重要。除此以外,他还发现了了二项式展开定理、牛顿恒等式等重要定理。
定义牛顿恒等式叙述如下2:
设F(X)=0的n个根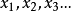 .对于
.对于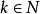 记
记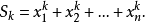 则有
则有
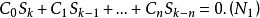
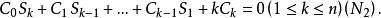
恒等式的证明对于一元二次方程,即:
F%5Cleft(x%5Cright)%3Dax%5E2%2Bbx%2Bc%3D0%2Ca%5Cne0%5Cleft(1%5Cright).
牛顿恒等式,设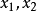 为方程两根,对于
为方程两根,对于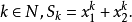 ,则有
,则有
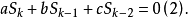
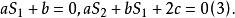
下面是(2)(3)式的证明:
(2)的证明:
由于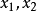 为方程二根,易得
为方程二根,易得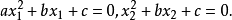
当k>2时,分别以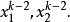 乘上这两个式子,得
乘上这两个式子,得
ax%5Ek_1%2Bbx%5E%7Bk-1%7D_1%2Bcx%5E%7Bk-2%7D_1%3D0%2Cax%5Ek_2%2Bbx%5E%7Bk-1%7D_2%2Bcx%5E%7Bk-2%7D_2%3D0.
相加两个上面两式,即可得(2)。
(3)的证明:
由韦达定理: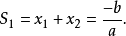 所以
所以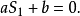 即(3)的一式成立,
即(3)的一式成立,
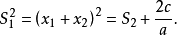
又因为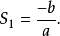 所以
所以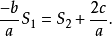 即(3)的二式成立。对于n>2其他情况,可以类比(2)(3)式加以证明
即(3)的二式成立。对于n>2其他情况,可以类比(2)(3)式加以证明
恒等式应用一、证明韦达定理1
由(3)式证明即可以看出:通过韦达定理既然可以推出(3)式,那么牛顿恒等式(3)式与韦达定理是等价的。通过逆推就可以证明韦达定理的正确性。
二、其他有用推论
1,通过方程1系数a,b,c,即可逐个确定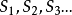
2, 如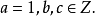 则
则
3,通过牛顿恒等式,也可以由a,b,c的奇偶性推知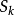 的奇偶性。
的奇偶性。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国