[科普中国]-机电耦合系数

机电耦合系数意思是压电振子在振动过程中，将机械能转变为电能，或将电能转变为机械能，这种表示能量相互变换的程度用机电耦合系数表示。

简介

其中，k是机电耦合系数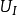； 是相互作用能密度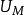； 是弹性能密度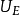； 是介电能密度。

常见的机电耦合系数有：

1、平面机电耦合系数 ：反映薄圆片沿厚度方向极化和电激励，作径向伸缩振动时机电耦合效应的参数

2、横向机电耦合系数K31：反映细长条沿厚度方向极化和电激励，作长度伸缩振动的机电耦合效应的参数。

3、纵向机电耦合系数K33：反映细棒沿长度方向极化和电激励，作长度伸缩振动的机电耦合效应的参数。

4、厚度伸缩机电耦合系数KT：反映薄片沿厚度方向极化和电激励，作厚度方向伸缩振动的机电效应的参数。

5、厚度切变机电耦合系数K15：反映矩形板沿长度方向极化，激励电场的方向垂直于极化方向，作厚度切变振动时机电耦合效应的参数。

压电换能器有效机电耦合系数的仿真分析借助ANSYS软件并选用Solid5（压电材料），Solid45（中间金属层），Circu94（电阻）3种元素类型建立压电换能器的有限元模型，通过谐振仿真分别求出压电装置的短路和开路谐振频率，得到其有效机电耦合系数。仿真结果表明，压电装置的有效机电耦合系数要小于压电材料的耦合系数，且与理论计算结果基本一致，仿真方法可有效地评价压电换能器的工作性能，并为后续实验提供理论指导。1

压电悬臂梁的有效耦合系数压电材料在受到外部作用力时产生变形，引起内部电荷发生相对位移而发生极化现象，这种现象称为正压电效应。反之，在受到电场力的作用下也会产生变形，称为逆压电效应。

压电悬臂梁由于中间金属层的作用，整个结构的弹性系数发生变化，同时压电材料在短路和开路时，由于电压的作用，弹性系数也有所不同，从而导致悬臂梁的固有频率改变。根据这一特点结合耦合系数的定义，采用开路－短路频率法可以求出压电悬臂梁的有效耦合系数。

压电换能器的有效耦合系数与压电材料的属性以及金属材料的弹性系数有关。1

有限元建模压电分析是一种涉及结构－电场的耦合分析，在采用ANSYS软件的耦合场分析功能对压电换能器进行有限元建模．分别选用Solid5（8 节点六面体耦合场元素）表示压电材料、Solid45（8 节点线性结构元素）表示中间金属层、Ciurcu94（电路元素）表示电阻．当双层压电悬臂梁受到外力作用而发生弯曲变形时（d31模式），上、下两层压电材料的变形方向不一样（上层拉伸，下层压缩），压电材料在表面附着电极，沿厚度方向极化，并在表面形成等势面。边界条件为一端固定，另一端自由．而在串联连接时，要求上层上表面和下层下表面的产生的电压极性相反，所以上下两层压电材料的极性也应相反．反之在并联连接时，两层压电材料的极性应一致。1

模态分析在 ANSYS 环境下进行压电耦合场分析时，要将压电材料表面的所有节点耦合至一个主节点。

模态分析的压电梁Z向位移云可知压电梁的Z向形由自由端至固定端逐渐减少。压电双层梁串联连接时，上层上表面的电压与下层下表面的电压绝对值相同，但极性相反。1

谐振分析为了计算压电换能器所产生的能量，可以对其进行动力学仿真分析。此时需将上、下两层压电材料的耦合主节点通过电阻元件（Circu94）相连。同时为了模拟周围环境的振动，对压电换能器的固定端施加恒定加速度进行谐振分析，可以得出压电悬臂梁的自由端位移，从而求出梁的应变和应力，然后根据压电方程就能估算所产生的电压。

在谐振仿真中，对连接的电阻值分别设置R=10E-20和R=10E20来表示压电换能器的短路和开路状态，同时分别设置不同的加速度幅值（a=2m/s2和a=4m/s2）来观察频率响应结果，得出短路、开路谐振频率。1

当R=0 时，压电换能器相当于电流源，且电压为零。而当R=∞时则相对于电压源，且电流为零。在施加不同的加速度条件下，压电悬臂梁的短路和开路谐振频率保持不变，分别为269Hz和276Hz，这表明短路、开路频率是压电悬臂梁的固有特性与外部施加的载荷大小无关，而且开路谐振频率与模态仿真的一阶频率结果相同。当施加的加速度幅值为2m/s2时，短路电流和开路电压分别为51μA和2.9V，而当加速度增大至为4m/s2 时，二者分别为 102μA和5.8V，这表明压电悬臂梁产生的电能与加速度成正比．因为随着加速度的增加（a=ω2Y ），悬臂梁的振幅（Y）增大，从而应变（应力）也相应的增大，由压电方程可知短路电流和开路电压也分别增大。

表明短路、开路自然频率的大小与外部施加载荷无关，有效耦合系数要小于压电材料自身的耦合系数。说明有限元仿真方法能够可靠地求出压电悬臂梁的有效耦合系数从而评价其工作性能，并且可以为后续的实验提供理论指导。1

机电耦合系数的标准计算方法的原理误差分析压电材料的机电耦合系数通常由谐振及反谐振频率之间的相对间隔确定。常用的IEEE标准计算公式，是由描述理想无损压电振子的电行为方程推导得出的。给出了压电材料的固有损耗产生的谐振及反谐振频率的偏移及由此引起的标准公式的误差。代替以往分析时常用的等效电路方法，采用把损耗考虑在内的严格的压电振子导纳或阻抗模型。分析结果表明 :由测得的谐振及反谐振频率用标准公式得出的耦合系数小于材料的固有耦合系数；误差随固有损耗的增加及耦合的减弱而增加。给出了较为详细的分析结果，确定了常用耦合系数标准公式的精确性及适用范围。2

有关机电耦合系数机电耦合系数，是指压电材料中与压电效应相联系的弹电相互作用能密度(亦称压电能密度)与弹性能密度和介电能密度乘积的几何平均值之比，是表示压电体机械能与电能耦合程度的参数，也是衡量压电材料压电性强弱的重要物理量。很多压电器件的性能指标，如压电滤波器的带宽、压电变压器的升压比、声表面波滤波器和延迟线的最佳带宽、叉指换能器的辐射阻抗、多条耦合器的最佳转换长度及金属带状线数目等，都直接与机电耦合系数有关。2

机电耦合系数与压电振子机电耦合系数不是压电材料的独立物理量，而是压电、弹性和介电参数的函数，所以它更能全面地表征压电材料的性质。压电材料生产厂家都对此参数非常重视，甚至只测量这一参数以衡量或比较不同材料的性能。由于压电振子的机械能取决于振子的形状和振动模式，不同的振动模式将有其相应的机电耦合系数。2

确定机电耦合系数k的方法确定机电耦合系数k的方法有多种。用实验方法确定压电振子的k值时常用 IEEE 标准方法，即由压电振子的谐振及反谐振频率间的相对偏差确定k值。常用的标准计算公式是由描述理想无损压电振子的电行为方程推导得出的，但对于机械品质因数Qm较低的压电振子则存在误差，且Qm值及k值愈小误差愈大。对不同振动模式的压电振子，以包含振子固有损耗的精确的阻抗或导纳模型为基础，进行k值的计算精度及应用范围的定量分析，并找出常用公式所适用的Qm值范围。2

分析了材料的固有机械损耗对特征频率的影响，进而讨论了损耗对由标准方法计算机电耦合系数的影响。当损耗大或耦合弱时(Qmk