[科普中国]-空间电荷波

空间电荷波理论建立了自由电子激光(FEL)的线性理论，导出了静磁Wiggler FEL中的空间电荷波方程，得到了空间电荷密度波和电流波，并详细地讨论了它们与一般的空间电荷波的区别。利用这些空间电荷波，导出了FEL的色散方程，并讨论了一些特殊的情况。提出了一个新的概念和建议。

概念非相对论电子注中的空间电荷波理论，已经详细地研究过。空间电荷波理论不仅能清晰地描述电磁扰动在电子注中传播的物理过程，而且可以用于建立各种电子与波互作用机理的线性理论，因此，有极重要的理论与实用价值。非相对论空间电荷波的理论，曾大大地推动了普通微波管及在非相对论条件下电子与波互作用机理研究的发展，我们相信，相对论空间电荷波理论系统的建立，也必将对相对论电子学的发展重要的推动作用。1

无引导磁场电子流的空间电荷波研究背景空间电荷波理论不仅能清晰地描述电磁扰动在电子注中传播的物理过程，而且可以用于建立各种电子与波的互作用机理的线性理论，因此，有极重要的理论和实用价值。传统的空间电荷波理论均是讨论真空中电子注的传递，随着高功率微波技术的发展，等离子体被引人微波器件中，等离子体的引人使微波管中的物理过程变得异常复杂，甚至在某些管中，由于等离子体的中和作用，利用电子注的磁自聚焦力，可实现电子注的无磁场聚束传输。等离子体中的波动过程已有人研究过，但在该环境下传输的电子注中传递的空间电荷波还未见报道。等离子体通道中的电子注，由于其传输特性与真空下大不一样，因而，在其上传播的空间电荷波亦有其自身的特性，详细地研究这种空间电荷波无疑对研制和开发等离子体微波器件有重要意义。

空间电荷波波动方程在圆柱坐标系（r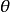， ，z）中，设电子注运动方向为z向，各扰动量有波动因子 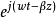形式，对Maxwell方程组进行处理并取波动方程交流部分的z分量，则

式中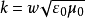： 是自由空间波数，E1z和J1z分别为电场矢量和电流密度矢量的Z向交变分量，ρ1为电荷密度的交变分量。在小信号条件下，假定高频扰动只使电子偏离平衡位置作微扰运动，则电子坐标可表示为：

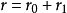
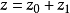
其中r0、z0为未扰运动坐标，r1和z1亦具有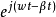形式。

空间电荷波方程的解对于空间电荷波方程，首先考虑自磁场可忽略的情况。假定电子注和等离子体均充满整个空间，由于填充等离子体的中和作用，相当于空间电荷力和密度下降，从而即使是一维情况，等离子体频率也下降。R为等离子体频率降低因子，可以证明R远远小于1。可见在填充等离子体条件下，R变得非常复杂，与等离子体中和因子有关。在空间电荷波的研究中，等离子体频率降低是一个重要的参数，真空磁约束下，该量主要与特征值有关，在等离子体约束下，不仅与特征值有关，而且与等离子体填充有关。这为用等离子体控制空间电荷波提供了基础。

由于等离子体的加入，空间电位发了变化，表达式虽不变，但与真空条件相比，其值已发生变化。由于空间电荷力的减弱，与真空对比，动电压值有所提高，动功率流定律形式不变。2

主动空间试验中空间电荷波向电磁波的转换研究背景在主动空间试验3(Active space experiment)中，电子束和空间等离子体相互作用一直是研究重点之一，利用电子束激发电磁波辐射因其独特的应用价值而备受关注。从20世纪60年代开始，陆续开展了一系列从空间飞行器发射电子束的主动空间试验，其中首次主动发射电子束试验(“Flash-1”和“Flash-2”) 便观测到了很强的无线电波辐射，其原因正是等离子体和电子束的相互作用。1975年“Araks”试验分别进行了代号为“North”和“South”的两次电子束发射，在电子束入射装置开启和关闭时观测到明显的电磁波辐射。20世纪90年代开展的“APEX(Active Plasma Experiment)”试验主要研究电子束侵入低电离层区域产生的人造极光、卫星附近等离子体和电子束的相互作用以及等离子体高频波振荡、卫星电荷中和的动力学过程等，试验过程中观测到包括哨声波和高频波的多频段波辐射。从已经开展的相关空间试验来看，对试验结果的解释异常复杂，有必要对电子束和空间等离子体相互作用激发电磁波的物理本质进行深入研究。

为此，众多科研人员做了大量工作。1965年Fainberg首先提出利用调制电子束穿越致密等离子体传输电磁波，在实验室条件下，利用电子束作为电磁波辐射源产生的波辐射已被观测到。Rogashkova的工作表明，在非均匀冷等离子体填充的波导中调制电子束可以激发出电磁波，而且电磁波辐射强度取决于电子束相对于等离子体粒子浓度梯度的运动方向，电子束流中空间电荷波的弛豫和电磁波的辐射特性与等离子体粒子浓度梯度有关。Krafft进行了有关电子束(包括调制电子束)和等离子体相互作用的试验研究，通过实验室模拟空间试验条件，证实了电子束在等离子体中激励哨声波的两种机制：切伦柯夫共振辐射和在电子束入射点产生的渡越辐射，并从理论上给予了解释。Anisimov对基于渡越辐射调制电子束和等离子体相互作用产生电磁波辐射以及影响辐射强度的各种因素分别进行了分析，引入了各向异性等离子体中渡越辐射形成区域横向尺度概念，并结合典型的主动空间试验参数计算了横向尺度大小，通常可达数十至数百米。在我们早期工作中开展了调制电子束在电离层中激发哨声波和高频波辐射的数值计算工作。

空间电荷波转换系数的理论推导试验和理论计算表明，从空间飞行器入射进电离层的电子束和等离子体相互作用，电子束流中的空间电荷波将转换为电磁波辐射。前面假设空间等离子体是均匀的，在这种情况下渡越辐射不可能发生，当电子束穿越等离子体浓度跃变区域时，渡越辐射就会出现。在主动空间试验中，这样的等离子体密度跃变区域不难找到，电子束入射装置附近的等离子体可满足该条件。完整求解空间电荷波转换为电磁波的系数很困难，下面分别就弱磁场近似、哨声波激发和低频近似三种典型情况分别计算空间电荷波向电磁波转换的系数。计算过程中假设两种等离子体交界处粒子浓度发生变化区域的横向尺度(假设为F)远小于等离子体-束系统中的任意波长。在具体试验中，这一条件很难满足，在数值计算过程中之所以做这样的假设，是因为对于较大尺度的非均匀等离子体区域，可以将其划分为分段区域，每个分段等离子体浓度变化区域的横向尺度可以满足上述条件。

假定背景等离子体浓度在电子束入射装置处(z=0)发生跃变：在z 0区域 np(z)=np2。考虑到离子浓度的影响，z =0 平面两侧的等离子体可以视为准中性，两侧区域的本征振动都由方程组描述，地磁场方向垂直于等离子体边界。研究电子束从z0等离子体区域后电子束的空间电荷波向等离子体特征波的转换。假定入射波位于 y-z 平面内，在y方向上等离子是均匀的，所以入射波在等离子体中激起的波对y的依赖关系和入射波相同。运用电磁场分量的一般边界条件和电子速度矢量各分量的连续性条件可以求解在等离子体浓度跃变区域空间电荷波转换为寻常波和非寻常波的系数Tk(k =1，2，3，4)。

数值计算和讨论作为验证，借助前期工作的数值计算方法，求解一种典型空间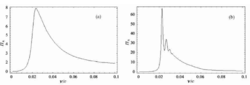试验条件下调制电子束产生的哨声波辐射。当不考虑电子束弛豫特性时，对应哨声波频段，求解各向异性均匀空间等离子体的色散方程可得到两组解，分别对应寻常波模和非寻常波模。对应非寻常波模色散方程的根为纯虚数，它所代表的电磁波在等离子体中将以指数形式很快衰减。对于寻常波模，计算所得电子束激发的哨声波前向辐射振幅大于后向辐射振幅。当不考虑电子束弛豫时，前向和后向渡越辐射以及前向切伦柯夫辐射方向图近乎一样。图1给出了满足哨声波辐射条件时前向辐射方向图。图1a中的峰值对应电子束在等离子体中满足切伦柯夫谐振条件时所产生的哨声波辐射总功率。对于非相对论电子束，后向辐射强度随着电子束速度的增加而增加。图1b是电子束弛豫长度为图1a中电子束弛豫长度 4 倍时得到的辐射方向图。图1a和1b对应的电子束弛豫长度分别为20m和80m。在其他参数不改变的情况下，适当增大电子束弛豫长度，将在一定程度上增加电子束产生的哨声波辐射强度，这是因为电子束弛豫长度的增加，将延长束和背景等离子体的作用时间，从而增大波辐射强度，同样由于作用距离的增加，导致辐射方向图中出现了多个峰值。

在“APEX”试验中，观测到很强的电磁波辐射，见图2。从图中可以看出，当电子枪开启时，观测结果中出现了明显的电磁波辐射，当电子枪关闭后，波辐射现象也随之消失，在电子枪工作过程中一直存在着不同强度的多频段波辐射。当电子束从电子枪入射进空间等离子体时，在航天器表面和空间等离子体的交界区域背景等离子体浓度存在着一个跃变，电子束与空间等离子体相互作用，电子束空间电荷波转换为较强的电磁波辐射。4

本词条内容贡献者为:

耿彩芳 - 副教授 - 中国矿业大学