在计算机科学中,形式语言是:某个字母表上,一些有限长字串的集合,而形式文法是描述这个集合的一种方法。形式文法之所以这样命名,是因为它与人类自然语言中的文法相似的缘故。
形式文法描述形式语言的基本想法是,从一个特殊的初始符号出发,不断的应用一些产生式规则,从而生成出一个字串的集合。产生式规则指定了某些符号组合如何被另外一些符号组合替换。
最常见的文法的分类系统是诺姆·乔姆斯基于1956年发展的乔姆斯基谱系,这个分类谱系把所有的文法分成四种类型:无限制文法、上下文相关文法、上下文无关文法和正规文法。四类文法对应的语言类分别是递归可枚举语言、上下文相关语言、上下文无关语言和正规语言。
简介上下文无关文法(英语:context-free grammar,缩写为CFG),在计算机科学中,若一个形式文法G = (N, Σ, P, S) 的产生式规则都取如下的形式:V->w,则谓之。其中 V∈N ,w∈(N∪Σ)* 。上下文无关文法取名为“上下文无关”的原因就是因为字符 V 总可以被字串 w 自由替换,而无需考虑字符 V 出现的上下文。一个形式语言是上下文无关的,如果它是由上下文无关文法生成的(条目上下文无关语言)。
上下文无关文法重要的原因在于它们拥有足够强的表达力来表示大多数程序设计语言的语法;实际上,几乎所有程序设计语言都是通过上下文无关文法来定义的。另一方面,上下文无关文法又足够简单,使得我们可以构造有效的分析算法来检验一个给定字串是否是由某个上下文无关文法产生的。例子可以参见LR 分析器和LL 分析器。
BNF(巴克斯-诺尔范式)经常用来表达上下文无关文法。1
形式定义上下文无关文法G是 4-元组:
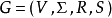 这里的
这里的
1.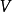 是“非终结”符号或变量的有限集合。它们表示在句子中不同类型的短语或子句。
是“非终结”符号或变量的有限集合。它们表示在句子中不同类型的短语或子句。
2.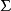 是“终结符”的有限集合,无交集于
是“终结符”的有限集合,无交集于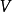 ,它们构成了句子的实际内容。
,它们构成了句子的实际内容。
3. 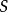 是开始变量,用来表示整个句子(或程序)。它必须是
是开始变量,用来表示整个句子(或程序)。它必须是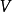 的元素。
的元素。
4. 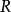 是从
是从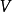 到
到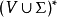 的关系,使得
的关系,使得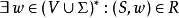 。
。
此外,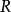 是有限集合。
是有限集合。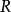 的成员叫做文法的“规则”或“产生式”。星号表示Kleene星号运算。
的成员叫做文法的“规则”或“产生式”。星号表示Kleene星号运算。
补充定义 1
对于任何字符串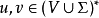 ,我们称
,我们称 生成
生成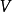 ,写为
,写为 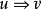 ,如果
,如果 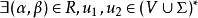 使得
使得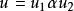 且
且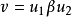 。因此v是应用规则
。因此v是应用规则 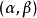 于
于 的结果。
的结果。
补充定义 2
对于任何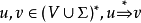 (或
(或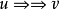 在某些教科书中),如果
在某些教科书中),如果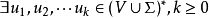 使得
使得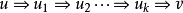 。
。
补充定义 3
文法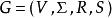 的语言是集合
的语言是集合
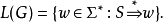
补充定义 4
语言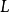 被称为是上下文无关语言(CFL),如果存在一个 CFG
被称为是上下文无关语言(CFL),如果存在一个 CFG 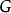 使得
使得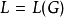 。1
。1
范式每一个不生成空串的上下文无关文法都可以转化为等价的Chomsky 范式或Greibach 范式。这里两个文法等价的含义指它们生成相同的语言。
由于 Chomsky 范式在形式上非常简单,所以它在理论和实践上都有应用。比如,对每一个上下文无关语言,我们可以利用 Chomsky 范式构造一个多项式算法,用它来判断一个给定字串是否属于这个语言(CYK算法)。2
参见上下文有关文法
形式文法
分析
分析表达式文法
随机上下文无关文法
本词条内容贡献者为:
张磊 - 副教授 - 西南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国