[科普中国]-曲线束

曲线束，是经典代数几何的常用术语。所有曲线束的曲线都通过它的两条基线的交点。所有曲线束的公共点（基线的交点）叫做曲线束的中心。

定义当给出了线性独立函数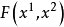 及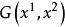 与及不同的参数值λ ，方程式

确定不同的曲线。

在各种参数值λ 的条件下，曲线 的集合构成一族曲线，它叫做曲线束。

曲线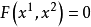及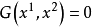 组成线束的基线，第一曲线属于参数值 λ=0 的曲线束。我们亦把第二曲线归入曲线束中，它是当参数 λ 无限增大时的结果。

为了使第二基线不是曲线束的例外情况，最方便地时以下列的比来代替参数λ

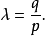那么方程式除去分母之后取得形式：

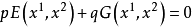曲线束的每一条曲线对应余数偶 p，q 以及所有与它们成比例的数。第一基线对应余值 q=0 与及任意 p 值，第二基曲线的对应值时 p=0，及任意的 q。

定理所有曲线束的曲线都通过它的两条基线的交点。

实际上，基线的交点坐标使函数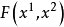 及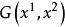 为零。因而带着任意的系数 λ 的它们的和也等于零，即是当参数 λ 未任意值时，方程式都成立。

这意味着，曲线当每一交点坐标都满足曲线束的任何曲线方程式，而这些交点本身式属于曲线束中所有曲线的。

曲线束的中心所有曲线束的公共点（基线的交点）叫做曲线束的中心。

通过平面上非曲线束中心的任何一点，有一而且只有一条曲线束的曲线。

设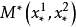 是平面上任意一点，但不是曲线束的中心。现在要证明，有一而且只有一条曲线束的曲线通过它。

以值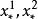 代入曲线束 (4') 的方程式，得

如果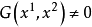 ，即是点 M* 不在第二基线 (5) 上，那么，由方程式 (a) 可以得到比值 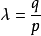，即

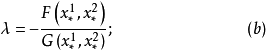这 λ 值决定曲线束中一条通过给与点点曲线。

如果 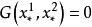及 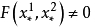，那么方程式 (a) 给出了 p=0。即是第二基线通过 M 点。

如果 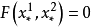及 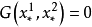，那么方程式 (a) 变为恒等式，p 及 q 为不定。在这种情况下坐标 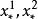满足基线 (5) 点两个方程式。而 M* 与曲线束的中心重合，这是与定理假设的条件矛盾的。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学