如果一个复数是某个系数不全为零的整系数多项式的根,则称此复数为代数数。不是代数数的复数,叫做超越数。超越数论研究数的超越性,其中对于欧拉常数与特定的黎曼ζ函数值之研究尤其令人感到兴趣。
定义以超越数为研究对象的数论分支之一。全体复数可分为两大类:代数数和超越数。如一个复数是某个系数不全为零的整系数多项式的根,则称此复数为代数数。不是代数数的复数,叫做超越数1。
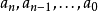 超越数是代数数的相反,也即是说若
超越数是代数数的相反,也即是说若 是一个超越数,那么对于任何整数都符合:
是一个超越数,那么对于任何整数都符合:

(其中an≠0)
发展史历史上第一个证明了超越数存在性的是法国数学家刘维尔(J.Liouville,1809~1882),他于1851年构造了一个数: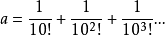 这个无限小数后来被称为“刘维尔数”。刘维尔成功地证明了这个数是一个超越数。在“刘维尔数”构造出来之后二十多年,数学家康托证明了:所有代数数的集合是可数的,即代数数的个数与自然数一样多!在此基础上,康托根据他的集合论中的另外一个结论——实数集是不可数的,得知复数集也是不可数的,因而进一步得到一个结论:必定存在不是代数数的复数,因此超越数必定存在!继刘维尔之后,数学家们为了证明某些具体的数的超越性付出了种种努力:1873年,法国数学家埃尔米特(C.Hermite,1822~l901)证明了自然对数的底e=2.7182818……是超越数。1882年,德国数学数学家林德曼(Lindemann,1852~1939)证明了圆周率π=3.1415926……是超越数2。
这个无限小数后来被称为“刘维尔数”。刘维尔成功地证明了这个数是一个超越数。在“刘维尔数”构造出来之后二十多年,数学家康托证明了:所有代数数的集合是可数的,即代数数的个数与自然数一样多!在此基础上,康托根据他的集合论中的另外一个结论——实数集是不可数的,得知复数集也是不可数的,因而进一步得到一个结论:必定存在不是代数数的复数,因此超越数必定存在!继刘维尔之后,数学家们为了证明某些具体的数的超越性付出了种种努力:1873年,法国数学家埃尔米特(C.Hermite,1822~l901)证明了自然对数的底e=2.7182818……是超越数。1882年,德国数学数学家林德曼(Lindemann,1852~1939)证明了圆周率π=3.1415926……是超越数2。
刘维尔开创了对超越数的研究,他发现无理代数数的有理数逼近的精密性有一个限度,借此他于1844年构造出历史上第一批超越数。早在1844年以前的一个世纪里,对无理数的研究已成为一个注意焦点。1744年,欧拉证明了自然对数的底e是无理数。1761年,朗伯证明了圆周率π是无理数。
1873年,埃尔米特证明了e是超越数,从而使超越数论进入一个新阶段。1882年,林德曼推广了埃尔米特的方法,证明了π是超越数,从而解决了古希腊的“化圆为方”问题。
19世纪超越数论的最高成就,是林德曼-外尔施特拉斯定理。
1900年,希尔伯特提出的23个问题中的第7问题是:如果是不等于0和1的代数数,是无理代数数,那么是否超越数希尔伯特曾预言,这个问题的解决将迟于黎曼猜想和费马大定理。盖尔丰德于1929年证明了:若是不等于零和1的代数数,是二次复代数数,则是超越数。库兹明于1930年把这个结果推广到是二次实代数数的情形。1934年,盖尔丰德和施奈德独立地对希尔伯特第7问题作出了肯定回答,此即所谓盖尔丰德-施奈德定理。由此可知,若是正有理数,则常用对数lg不是有理数,便是超越数;更一般地,对非零代数数,,,,若ln,ln在上线性无关。
超越数论的最新发展使用着来自交换代数、代数几何、多复变函数论、甚至上同调理论的方法,正处于活跃之时。
超越数的意义证明某些数是超越数有着重大的意义,比如说π的超越性的证明就彻底地解决了古希腊三大作图问题中的化圆为方问题,即化圆为方是不可能的。判断某些给定的数是否超越数实在是太困难了,为了获得上述结果,一个多世纪以来,数学家们付出了艰苦的劳动。即便如此,这个领域仍旧迷雾重重。比如说,现今仍然无法断定像e+π和这样的数到底是代数数还是超越数。
了解超越数实数中除代数数以外的数,亦即不满足任一个整系数代数方程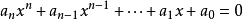 (n为正整数,
(n为正整数,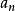 ≠0)的数。理论上证明超越数的存在并不难,而且可知超越数是大量的。但要构造一个超越数或论证某个数是超越数就极为困难。现今只有少量的数如π,e,等的超越性得到了证明,对其他一些有兴趣的数的超越性的研究是数学家十分关注的事。
≠0)的数。理论上证明超越数的存在并不难,而且可知超越数是大量的。但要构造一个超越数或论证某个数是超越数就极为困难。现今只有少量的数如π,e,等的超越性得到了证明,对其他一些有兴趣的数的超越性的研究是数学家十分关注的事。
例子超越数的例子包括:
钱珀瑙恩数
刘维尔数
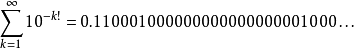
它是第一个确认为超越数的数,是于1844年刘维尔发现的。
 (参见:e)。
(参见:e)。
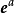 ,其中
,其中  是除0以外的代数数。
是除0以外的代数数。
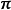 (参见:圆周率)
(参见:圆周率)
林德曼-魏尔斯特拉斯定理,1882年,注:因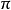 是超越数而证明尺规作图中的“化圆为方”的不可实现性。
是超越数而证明尺规作图中的“化圆为方”的不可实现性。
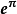 (参见:e的π次方)
(参见:e的π次方)
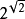 (参见:2的√2次方)。
(参见:2的√2次方)。
更一般地,若 为零和一以外的任何代数数及
为零和一以外的任何代数数及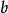 为无理代数数则
为无理代数数则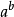 必为超越数。这就是格尔丰德-施奈德定理。
必为超越数。这就是格尔丰德-施奈德定理。
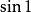 (参见:正弦)
(参见:正弦)
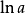 (参见:自然对数),其中
(参见:自然对数),其中 为一不等于1的正有理数。
为一不等于1的正有理数。
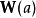 (参见:朗伯W函数),其中
(参见:朗伯W函数),其中 为一正有理数。
为一正有理数。
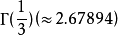 ,
,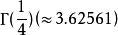 及
及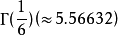 (参见伽玛函数)。
(参见伽玛函数)。
所有超越数构成的集是一个不可数集。这暗示超越数远多于代数数。可是,现今发现的超越数极少,甚至连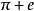 是不是超越数也不知道,因为要证明一个数是超越数或代数数是十分困难的。
是不是超越数也不知道,因为要证明一个数是超越数或代数数是十分困难的。
超越数的证明,给数学带来了大的变革,解决了几千年来数学上的难题——尺规作图三大问题,即倍立方问题、三等分任意角问题和化圆为方问题。随着超越数的发现,这三大问题被证明为不可能。3
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国