[科普中国]-法方程

法方程是测量平差计算中的一个重要的方程，是由平差函数模型线性化后的方程式、以及在VTPV=min的条件下所导得的方程式合并而成的联立方程组。

概念法方程是测量平差计算中的一个重要的方程。它是由平差函数模型线性化后的方程式，以及在VTPV=min的条件下所导得的方程式合并而成的联立方程组。在各种平差函数模型中，方程式的个数总是少于所求未知量的个数，是多解方程，解不惟一，通过法方程则可求得既满足所有方程式，又满足VTPV=min的一组惟一解。例如，就附有限制条件的条件平差法而言，方程组：

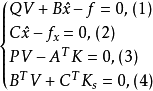就是它的总法方程，或称基础方程。其中(1)，(2)两式是其函数模型线性化后的方程式，(3)，(4)两式是在VPV=min”的条件下按条件极值导出的方程式。K和Ks是求条件极值时分别对应于(1)式和(2)式的拉格朗日乘数向量，在测量中习惯称为联系数向量。若利用(3)式消去V，则得：1

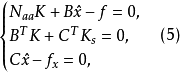(5)式称为法方程，其中Naa=AQAT。其他各种平差方法的总法方程和法方程都可由(1)～(4)式和(5)式简化而得。

各种平差方法的法方程，其系数阵都是对称满秩方阵。但在选取与定位有关的参数进行参数平差时，若网中无起算数据或起算数据不足，误差方程的系数阵列不满秩，即产生基准秩亏，则法方程的系数阵将是奇异的。

秩亏网平差秩亏网平差亦称自由网平差。平差计算中的方法之一。它是当测量网选取与定位有关的参数进行参数平差时，其误差方程式的系数阵为列不满秩的一种平差方法。引起系数阵列不满秩的原因有：

1.网中的必要观测数据不足，使网的形状无法确定；

2.网中无必要的起算数据，使网的位置、方位和尺度无法确定。

实际工作中，在测量网中总是要进行多余的观测，因此通常所称的“秩亏网”都是指无必要起算数据的测量网。以测量网点坐标为参数的误差方程为：

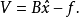由于网中无起算数据，R(B)=t