[科普中国]-界面能

晶界上由于原子排列是畸变的，因而自由能升高，这额外的自由能称为晶界能。小角度晶界的能量主要来自位错能量（形成位错的能量+将位错排成有关组态所作的功）。而位错密度取决于晶粒间的位向差。所以小角度晶界能g（单位面积的能量）也和位向差q有关。1

简介晶格的表面实质上是晶体与其蒸气之间的界面，表面能便是这两相之间的界面能。晶体内部界面上的原子周围环境也与其他原子不同，因而界面的自由焓也高于晶粒内部。单位面积界面的自由焓称为界面能，常用γ表示。

对于纯金属及单相合金，大角度晶界界面能最高。小角度晶界界面能较低，而且位向差越小，界面能越低。共格孪晶界界面能最低。对于合金中的相界，非共格相界界面能最高，共格相界界面能最低，半共格相界界面能居中。2

界面能的各向异性19世纪末，人们已开始研究晶体的外观形貌。Gibbs首先指出，晶体体积恒定，且无外力作用时，晶体的几何形状使总表面能为最小。Wulff进一步指出，晶体在逼近平衡时将调整自己的形状，以使其本身的总表面能降至最小。显然，晶体的表面能是晶体取向的函数。在晶体中，原子排列的情况是随晶面而异的，这也决定了界面能的各向异性。界面能的各向异性通常用γ能级图和Wulff结构图来表示。

Gibbs和Wulff定理可用下式描述，在恒温、恒压平衡状态下，一定体积的晶体具有的总表面能应最小，公式为： 最小值。3

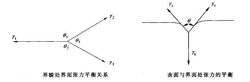
界面能的测量界面张力平衡法大多数界面能的测量可利用界棱处3个界面张力的平衡关系进行。界棱处的3个两面角可由实验直接测定，根据平衡关系（如下左图）：

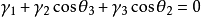或

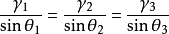当已知其中一个界面能，另两个便可算出。如已知某种金属的表面能，也可利用表面张力的平衡求得界面能。一光滑表面在惰性气体或真空中长时间加热，为保持界面张力平衡，通过原子扩散，在界面与表面相接部分形成热蚀沟，如下右图所示。

沟槽处界面张力的平衡是

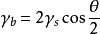
测出沟槽张角θ，可求出界面能γb。如已知γb，可求得表面能γs。α角的测量可以金相法在垂直表面的截面上进行，也可用干涉显微镜直接在表面上进行。4

测量界面能的动力学方法金属中发生的许多过程都与界面能有关。界面能在这些过程中起着促进或阻碍作用。在这些过程的动力学表达式中包含着界面能。因此，如果表达式中的其他参数可测，便可求得界面能。例如可利用第二相颗粒聚集长大的动力学方程测定基体相与第二相之间的相界能。方程具有以下形式

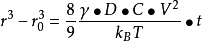式中，γ为相界能，r0为开始长大前第二相颗粒的平均半径，r为温度T时间t时颗粒的平均半径，D为溶质在基体相中的扩散系数，C为温度T时溶质在基体相中的平衡溶解度，V为第二相的原子体积，kB为波尔兹曼常数。由于表达式在推导时作了一些假设，因此测量的数据与其他方法测得者有较大偏差。4

界面能的作用界面能是形核的阻力，在形核过程中它起很重要的作用。在固态相变中，新相和母相均是晶体，因此新相和母相在界面上的原子排列结构有可能完全匹配（完全共格界面）、不完全匹配（半共格界面）以及混乱的完全不匹配（非共格界面）三种情况。显然，两相间界面能随着界面两侧原子排列匹配程度加大而减小，两相在界面上匹配程度取决于两相在界面上晶面间的错配度艿的大小。形核时总希望有最低的总表面能。非共格的界面能太高以至于基本上不可能形成全部界面都是非共格界面的核心。如果调整核心和母相的取向关系，使核心出现尽量多的共格或半共格界面，这样会减小形核功，形核过程便易于进行。如果母相和稳定的新相的晶体结构差异很大．以至于不管新、母相如何调整取向关系也不可能形成共格的低能界面，则有可能形成与母相呈共格界面关系的另一种亚稳定相晶核。对于共格界面，界面两侧原子排列的间距差异是由两相的弹性应变能承担的。当新相长大到较大尺寸时，引起的弹性应变能太大，将会在界面上引入位错网络来降低弹性应变能，这时界面变成半共格界面。新相长大到更大尺寸时，共格（半共格）关系使总界面能的减少不足以补偿维持共格（半共格）所引起的弹性能或结构能，新相和母相间就失去共格关系。另外，如果转变过程中母相因再结晶或晶粒长大改变了母相的晶体取向，也会使新相和母相间的共格关系丧失。

新相和母相的结构不同时，如果调整新相和母相的取向关系可能出现1个低能的共格或半共格界面，一般来说，不再会有其它匹配良好的面。

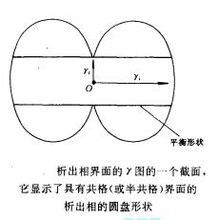
即是说，即使新相和母相选择一定的取向关系可以出现共格或半共格界面，这样的取向关系也不可能使1个三维的晶核的所有界面都是共格或半共格的，还一定会有部分界面是高能的非共格界面。如果作出新相界面取向和界面能的关系图（γ图），它大致地成球状，但在垂直于共格（半共格）面方向有两个很深的脐点，如下图所示。按照Wulff法则可以知道新相的平衡形状是圆盘状，圆盘面平行于新相和母相良好匹配面。圆盘的直径和厚度的比值等于非共格界面能γi和共格（半共格）界面能γC的比值（γi/γC）。实际观察到的析出相的形状可能偏离这些理想形状，因为上面的讨论没有考虑体积弹性应变能；另外，在长大时由于共格（半共格）面的迁移速度比非共格面低，所以圆盘的直径和厚度比要比上述的大得多。

根据上面讨论的道理可以知道，新相往往在平行于母相的特定面析出，母相的这个面称为惯习面（Habit Plane，也有人译为惯析面）。同时又可以知道片状析出相一般都会和母相有一定的取向关系。有取向关系的典型例子如：Al（母相，fcc结构）-Ag2Al（析出相，hcp结构），它们间的取向关系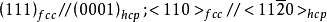是 ，惯习面是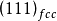 。又如Al-Cu合金中的AI（母相，fcc结构）-θ（析出相，tet结构），它们间的取相关系是 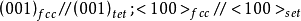（001），惯习面是 。

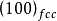有一些体系它们之间仅有匹配好的方向，例如Fe-Cu系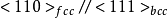， ，析出相是针状的。

如果新相界面的γ图是各向同性的，即γ图近似球状，这样析出的新相核心的是球状的。有两种情况新相界面取向的γ图是球状的：其一是当母相和新相的结构相同，二者的点阵常数又相近的情况，例如AI-Ag合金中脱溶析出的“G.P区”就是球状的；其二是当母相和新相之间完全找不到可以匹配良好的晶面和晶向的情况，这时新相界面的任何取向都只能是非共格界面，核心也是球状。5

界面能对界面稳定性的影响固液界面在偶然因素干扰下产生凸缘，因而增加了固液界面的面积，这就使固液界面的总界面能增加了。我们知道，界面能的增加就提高了系统的自由能。而在平衡条件下系统的自由能有缩小的趋势，于是固液界面面积就趋于缩小，这将促使平坦界面上的凸缘趋于消失。因而界面能是促进生长界面稳定的因素。理论分析表明，如果干扰较小（在干扰初期），凸缘的尺寸小于微米数量级，则界面能对界面稳定性的贡献较大。如果凸缘已经长大了，其尺寸超过微米数量级，则表面能的作用就不大了。6

界面能对聚集形态的影响维塞克（T．Vicsek）在DLA模型的基础上，在界面生长中引入表面张力，考虑了吉布斯-汤姆逊效应对界面生长的影响。当两平衡的界面是曲面时，其平衡温度和浓度等参量是界面曲率的函数。对于一个随机起伏、不断分叉的生长界面，其界面上各点的化学势将是不等的，因而导致沿着生长界面的质量和能量的输运。其结果是生长界面上一些细微的沟槽和港湾被填平，整个界面趋向平滑。在具体的计算机模拟实验中，维塞克让粒子以无规行走的方式（对应于非局域的扩散场）来到聚集簇附近，这对应于DLA的传输过程。但在界面过程中补充了两个规则：①假设粒子的粘着几率是与表面的局域曲率有关，如果粒子不粘着于表面，就将继续扩散；②当粒子一旦着陆以后，就将弛豫到附近的能量更低的坐位（具有最大数目被占近邻的坐位）。这一方法实际上结合了两种方法：一是对于个别聚集粒子的扩散运动的直接模拟；另一是对于凝固问题的连续统方程的蒙特卡罗模拟。这里的粘着几率与界面曲率有关相当于连续统理论中吉布斯一汤姆逊关系式确定的边值条件；而表面弛豫用来模拟凝固表面上分子的调整位置的动力学过程，这样可以导致空洞的消失，更加致密的基体和光滑的表面。

为了模拟定向凝固，人们可以让粒子沉积在一条线上（而不是一个点上）；为了模拟界面以一速率运动，可以引入有偏向的无规行走，即定义朝向界面运动的几率P大于离开界面运动的几率，所得结果如图所示。这里呈现的胞状界面的图像与实验观测的结果颇为相似。6

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学