[科普中国]-多导体系统

多导体系统是3个或更多个导体组成的静电系统。若这样的导体系统中总电荷代数和为零，便称之为独立的多导体静电系统。系统特点是与外界没有联系。

概念系统定义多导体系统 （system of conductors ）是指多个导体组成的静电系统。若这样的导体系统中总电荷代数和为零，便称之为独立的多导体静电系统。1

系统特点在多导体系统中，所有电力线全部从此系统内的 带电体发出并终止在系统内的带电体上，与外界没有联系；导体间的电场分布只与系统内各带电体的形状、尺寸、相对位置及电介质有关而与系统外的带电体无关。

导体之间的关系对于n+1个导体组成的静电独立系统

q0+q1+q2+…+qn=0

式中q0、q1、q2、…、qn分别为各导体的电荷，设q0属于电位为零的参考导体。若电介质的介电常数不随电场强度而变化，则导体系统便是线性的。对于静电独立线性系统，各导体的电位φk与电荷qj(j，k=1，2，…，n)有以下关系：

φ1=α11q1+α12q2+…+α1nqn

φ2=α21q1+α22q2+…+α2nqn

………………

φn=αn1q1+αn2q2+…+αnnqn

或以矩阵形式表示为

[φ]=[α][q]

式中α为电位系数。αkk 称为导体K的自电位系数；αjk 称为导体j与K的互电位系数，且αjk=αkj。所有各电位系数均为正值。由上式可导出电荷与电位间的关系为 q1=β11φ1+β12φ2+…+β1nφn

q2=β21φ1+β22φ2+…+β2nφn

………………………

qn=βn1φ1+βn2φ2+…+βnnφn

其矩阵形式为

[q]=[β][φ] [β]=[α]-1

式中β为感应系数；βkk为导体K的自感应系数，又称电容系数；βjk为导体j与K的互感应系数，且βjk=βkj。βkk >0，但βjk≤0。经过一些变换，还可得出电荷与电压间的关系为

q1=C10φ1+C12(φ1－φ2)+…+C1n(φ1－φn)

q2=C21(φ2－φ1)+C20φ2+…+C2n(φ2－φn)

…………………………

qn=Cn1(φn－φ1)+C(φn－φ2)+…+Cn0φn

及

Ck0=βk1+βk2+…+βkn

Cjk=－βjk

式中C为部分电容；Ckk为自部分电容；Cjk为互部分电容，且Cjk=Ckj。部分电容均为正值。使用部分电容在研究导体系统的电位与电荷关系时，可以将多导体系统化为等效的电容电路来分析。

电位系数的单位为1/法(拉)，感应系数与部分电容的单位均为法(拉)。3类系数均只与导体的形状、尺寸、相对位置及电介质有关，在线性介质中，与系统的电荷及电位无关。

多导体系统的广义Collin原则在电磁变分领域中，上下界的估值一直是研究的重要问题。Collin由研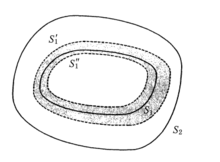究二维导体传输线之间的电容变分稳定而提出了著名的Collin原则。它可以简单描述如下：如图1所示，S1作为内导体，S2作为外导体一起构成双导体传输线。其单位长度的电容记为C0。现设S′1在S1的外部，而S″1在S1的内部，并分别假设S′1与S2和S″1与S2之间的电容为C′和C″，则文献证明由变分极值原理可知：

C′> C0 >C″

换句话说，C′和C″可分别作为电容精确值的上界和下界估计。文献2给出了Hermite算子的本征值估值定理。值得指出，林为干推广了Collin原则的应用，并得到了一批各种传输线电容和特性阻抗的很好近似公式。

多导体系统Collin原则图2给出典型的由n个孤立导体构成的多导体系统。作为一般情况，每个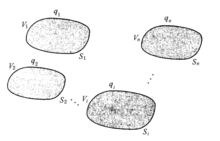导体上分别加上电压V1，V2， …，Vi， …，Vn，而储存的电荷则分别为q1，q2， …qi， …，qn。于是可写出[C] [V] =[q]。

其中[C]为电容矩阵，且有[C]T=[C][ ]T，表示矩阵转置。和孤立导体的情况类似，[C]是空间导体分布和媒质分布的函数，与[V]和[q]无关，它是特征矩阵。

多导体系统应用实例作为典型例子，研究如图3所示的对称平行方杆(W×W)的奇模电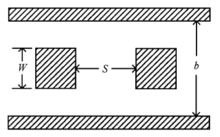容即C([1，-1])。假定我们知道对称平行圆杆的相关数据。

根据广义Collin原则，本文采用与方杆等周长的圆作为模式电容的逼近值。其物理意义是：对于二维情况，在相同的电压条件下，若假定方杆和圆杆电荷都是均匀分布，则两者有相同的电荷(二维分布于周长，且z=1)。于是有相同的电容，这是广义上的平均意义。

研究结论本文把Collin变分原则推广到孤立导体和多导体系统。利用广义平均意义：等表面积的导体估计电容逼近值，不仅方法简单，而且从应用实例看出，其估计值很靠近于真实值。这一工作将有助于快速估计复杂系统的电容，同时确切了解问题的上下界。3

复杂多导体系统电磁瞬态快速计算方法电力系统中包含大量的多导体系统，如变压器、电抗器及接地网等，由于系统中导体数量庞大，这类系统将对应一种大规模耦合复杂电路模型，从而导致电磁瞬态仿真运算量巨大，瞬态计算复杂度高，快速求解困难。波形松弛法是一种迭代求解方法，其主要思想是通过将系统分解成若干个子系统然后迭代求解。由于子系统相对于整个系统规模小很多，减小了内存的占用，从而使得大规模电路瞬态仿真成为可能。波形松弛法首次被用于电路分析的是Lelarasmee等人。文献4在利用波形松弛法求解RC梯形电路时发现算法的收敛速度具有频率相关特性，并提出了一种用于改善RC梯形电路低频收敛特性的改进波形松弛法。Gander等人为了改善波形松弛法的收敛速度，提出了基于轴向分解的波形松弛法。Nakhla教授领导的课题组近年来针对印制板互连线系统的高效求解开展了一系列研究工作，提出了基于横向分区的波形松弛技术(Waveform Relaxation and Transverse Partitioning，WR-TP)。该方法的基本思想是将传输线进行横向维数截断，即将多导体传输线分解为多根单导体传输线，进而通过迭代方式实现仿真计算。进一步研究发现，网络中参数的耦合越强，WR-TP达到收敛所需要的迭代次数越大，因此对于强耦合电路，WR-TP的计算效率较低。针对该问题，文献基于系统分解思想提出了一种基于重叠分区的强耦合多导体传输线系统的新型波形松弛法，该方法根据导体之间的耦合强弱关系实现整个系统分解，将耦合较强的导体划分在同一个子系统中，子系统间存在重叠区域，算例分析表明这种重叠分区的处理方法可加快收敛速度。

由此可见，基于重叠分区的波形松弛法其收敛速度与网络分解后各个子网络间的耦合强弱密切相关，但现有文献中采用的重叠分区技术仅是通过数值仿真实验对算法的收敛速度进行简单讨论，并没有给出网络分区的方法和依据。考虑到网络函数关于耦合参数的导数体现了耦合参数对网络输出的宏观影响，本文提出了一种基于网络灵敏度分析的电路耦合强度的判别方法和网络分区技术，并基于该方法实现了具有快速收敛速度的多导体系统波形松弛法，最后通过算例验证了算法的正确性与高效性。

多导体系统的PEEC模型PEEC模型是建立多导体系统电路模型的一种非常有效方法，其是将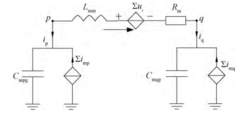导体视为细线结构，并依据导体尺寸与瞬态激励的波长关系将各导体划分为若干线元，线元之间的电磁耦合则通过部分电感和部分电容进行描述。每一段线元的PEEC模型拓扑如图4所示，其中与电感支路串联的受控电压源表示其它单元与本单元间的互电感耦合，与电容支路并联的电流源表示其它单元与本单元的互电容耦合。

基于灵敏度的多导体系统耦合强度分析网络灵敏度是指“网络函数”对“元件参数”的敏感程度，网络中导体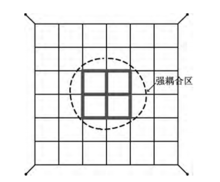间互电感和互电容等耦合参数的灵敏度大小反映了耦合参数对冲击特性的影响。由于绝对灵敏度不能确切的表明参数对网络特性的影响程度，所以通常采用相对灵敏度，其为网络函数的相对变化量与元件参数的相对变化量的比值。

网络灵敏度的计算方法一般有伴随网络法、导数网络法等方法，前者更加适合大型网络，所以本文基于伴随网络法推导了网络函数关于耦合参数的灵敏度计算公式。从互电感和互电容的灵敏度分析可以发现，网络中在以田字格型方块内的导体之间耦合较强，如图5所示。因此，在对网络分区时应将此强耦合区域置于同一个子网络中，即子网络之间的重叠区域应包含此强耦合区。

研究结论波形松弛法的主要思想就是将大网络分成多个子网络进行迭代计算，但分区应尽可能不破坏导体之间的强耦合关系。虽然重叠分区能够很好地保留导体之间的耦合，重叠部分越多收敛速度越快，但重叠区域越多将导致各子个网络的计算复杂度增加，因此合理的重叠大小能够进一步提高计算效率。本文基于灵敏度分析提出的多导体系统瞬态计算的分区方法，可有效判别导体之间的强弱耦合关系，基于这种强弱耦合关系对整体网络进行分区，并结合波形松弛法进行迭代计算，能够大大的提高计算效率。本文方法的正确性和高效性均通过算例和实验得到了验证。本文方法可直接应用于求解如变压器、 电抗器绕组、 变电站地网、 高速铁路综合接地系统等含有大规模多导体系统的电磁瞬态计算。此外， 由于网络分解后各个子网络的内部求解相互独立，可结合并行计算进一步加快求解速率， 这也是本文后续将开展的工作。5

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学