[科普中国]-强稳定性

强稳定性是一种较强的稳定性质。如果能证明有有界解是强稳定的，那么它就是概周期解；反之，在微分方程满足标准假设时，方程的任何概周期解都是强稳定的。

简介强稳定性是一种较强的稳定性质。

如果对任给 ε>0 ，存在 δ(ε)>0 ，使得只要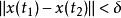，便有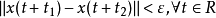，称解 x(t) 是强稳定的。

如果能证明有有界解是强稳定的，那么它就是概周期解；反之，在微分方程满足标准假设时，方程的任何概周期解都是强稳定的。1

可继承性(inherited property)

可继承性是关于一致概周期微分方程解的一种重要性质。

如果一致概周期微分方程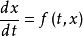的解 φ(x) 相对于其他解具有性质 P ，若， 而ψ(t) 相对于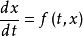的解也具有性质 P ，则称性质 P 是可继承的。也就是说，若解φ(x)具有可继承的性质 P ，那么，性质 P 在算子 Tα 的作用下是自封的。

通常往往利用有界解的某些稳定性质来建立有界解的概周期性，诸如一致稳定、一致渐近稳定、完全稳定或壳扰动下的稳定等，这些稳定性质在方程满足标准假设时都是可继承的。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学