使泛函达到极值的变元函数称为极值函数,若它为一元函数,通常称为极值曲线。极值也称为相对极值或局部极值。
简介极值是变分法的一个基本概念。泛函在容许函数的一定范围内取得的最大值或最小值,分别称为极大值或极小值,统称为极值。使泛函达到极值的变元函数称为极值函数,若它为一元函数,通常称为极值曲线。极值也称为相对极值或局部极值。1
欧拉方程的积分曲线(Euler equation)
欧拉方程是泛函的极值函数满足的微分方程,假设 F(x,y,y') 关于变元是二次可微的,函数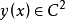 且满足边界条件
且满足边界条件
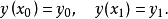 那么泛函
那么泛函
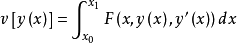 取极值的必要条件是:
取极值的必要条件是: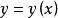 是微分方程
是微分方程
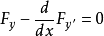 或
或
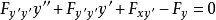 的解。这个方程称为欧拉方程。
的解。这个方程称为欧拉方程。
欧拉方程的积分曲线称为极值曲线。对于形如
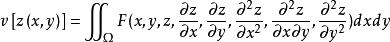 的泛函,它相应的欧拉方程为
的泛函,它相应的欧拉方程为
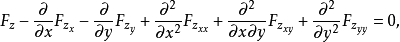 式中
式中
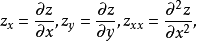
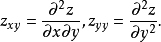
局部极值设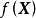 是欧氏空间
是欧氏空间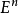 中某一区域
中某一区域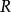 上的n元实函数,对于
上的n元实函数,对于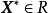 ,若存在某个
,若存在某个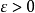 .使得所有
.使得所有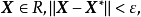 ,满足
,满足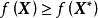 ,则称
,则称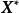 为
为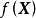 在R上的局部极小点(或称相对极小点),
在R上的局部极小点(或称相对极小点),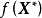 为局部极小值。若对于所有
为局部极小值。若对于所有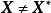 ,且与
,且与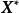 的距离小于
的距离小于 的
的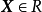 ,有
,有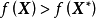 ,则称
,则称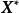 为
为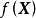 在R上的严格局部极小点,
在R上的严格局部极小点,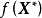 为严格局部极小值。
为严格局部极小值。
设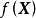 是欧氏空间
是欧氏空间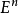 中某一区域
中某一区域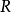 上的n元实函数。若点
上的n元实函数。若点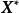 对于所有
对于所有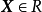 ,都有
,都有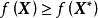 ,则称
,则称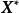 为
为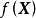 在
在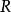 上的全局极小点,称
上的全局极小点,称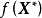 为全局极小值。若对于所有
为全局极小值。若对于所有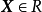 ,且
,且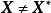 ,都有
,都有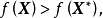 则称
则称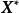 为
为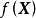 在R上的严格全局极小点,
在R上的严格全局极小点,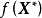 为严格全局极小值。
为严格全局极小值。
对于极大点与极大值,不难仿上给出相应定义。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国