[科普中国]-高次谐波效应

单一频率的基频波入射到非线性介质后，由于高次非线性电极化系数的耦合效应而产生频率为入射光波(基频波)的三倍、四倍甚至更高倍的光波辐射，这种非线性光学现象称为高次谐波效应(higher harmonic effect)，产生的光波称为高次谐波(higher harmonic)。1962年首次在二氟化钙晶体中，对红宝石的 6943Å激光谱线进行三倍频获得2314Å的三次谐波。 高次谐波通常是逐次利用低阶的非线性电极化项而产生的。例虹1.06μ的基频波先由磷酸二氢钾倍频；再用磷酸二氘钾倍频而获得四次谐波——2661Å的紫外光；最后再以高压气体氖进行五倍频得到532Å的相干辐射，这相当于1.06μ的基频波的20次高次谐波。在准分子激光器及1971年氢分子真空紫外激光器制成之前，高次谐波技术是获得相干真空紫外光波的唯一有效方法，它可望发展成为实现相干X光的重要手段1。

空间效应在具有反射层的堆中用脉冲中子源法测得的反应性将与源和探测器的空间位置有关。例如马斯特斯(Masters)和卡第(Cady)在用普通水作慢化剂和反射层的临界装置上所进行过的脉冲中子实验表明：按三种不同方法一简单面积法、外推面积法和G-R方法——测得的反应性随探测器位置的变化而变化。变化曲线如图1所示。

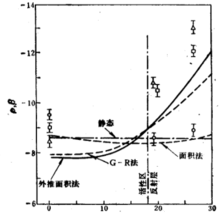
(实验：O面积法；口G-R法；△外推面积法)

这一空间效应是由两部分原因引起的：第一部分原因是由于存在着高次谐波，第二部分原因是由于瞬发中子通量的空间分布与缓发中子通量的空间分布不同。分别介绍如下。

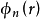高次谐波效应无论是裸堆还是带反射层的堆，在次临界状态下都存在着高次谐波。如前所指出的，堆内的中子通量可用谐波展开。

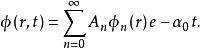
各阶高次谐波的空间分布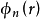都不相同，因此不同点处的各阶高次谐波的贡献亦不相同。例如，在裸堆中，设脉冲中子源放在堆芯中心，则在堆内不同点的高次谐波功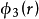与都不同，如图2所示。在不同点测得的中子通量随时间的变化曲线也会不同。例如在图2中所示的0点，三次谐波和五次谐波可能相互抵消，因此基波占主导，在a点，三次谐波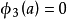，只有五次谐波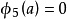及高于五次的谐波存在，在b点，三次谐波与五次谐波均不为零。因此，如果探测器与源的位置选择适当，可以消除或减少高次谐波的影响。

例如，对于一个高H半径为R的圆柱形裸堆，将源可放在堆的顶部中央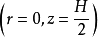处，如图3所示。源中子所激励的径向中子通量的谐波与轴向中子通量的谐波的空间分布，如图中曲线所示。如果把探测器放于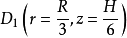处，则轴向通量的三次谐波与径向通量的三次谐波在该处均为零。如果把探测器放于处，则轴向通量的二次谐波与径向通量的三次谐波在该点均为零。另一种方法是同时将两个相同的探测器分别放在处和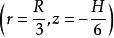处进行测量，然后将测得的信号相加。这样，在合成的信号中，轴向通量二次谐波的贡献互相抵消，而轴向通量的三次谐波和径向通量的三次谐波均无贡献。以上只示例地介绍了在实验中如何消除或减少高次谐波的方法。在数据处理中亦可采用适当方法来消除或部分消除高次谐波的影响，如外推面积法，G-R方法等。

动态畸变效应在均匀裸堆中，瞬发中子通量的空间分布和缓发中子通量的空间分布是相同的。但在带反射层的反应堆中，各阶谐波的瞬发中子通量的空间分布与缓发中子通量的空间分布是不相同的，即。此种现象称为动态畸变，它只发生于堆处于动态情况。

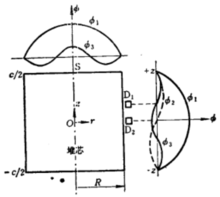
图3 在圆柱形裸堆内由顶端脉冲源S所激励的中子通量谐波随r和z的变化

在描写中子运动的中子动态方程中，中子密度随时间的变化率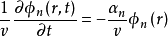，这一项可以用一个假想的等效宏观吸收截面的吸收项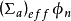来代替。这样动态方程就可转化为以总吸收截面为的静态方程。对缓发中子， 由于其衰减常数都很小，一般在反射层中等效宏观吸收截面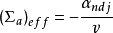的绝对值远比反射层介质的宏观吸收截面小，可忽略，因而缓发中子通量的空间分布接近静态的中子通量分布。但瞬发中子的衰减常数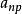较大。在反射层中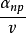和相比不能忽略，则等效的总吸收截面为，因而在反射层中瞬发中子通量的空间分布不等于静态的中子通量分布。由于在堆芯与反射层交界面上中子通量与中子流密度的连续性条件，相应堆芯内的瞬发中子通量的空间分布也与堆芯的静态中子通量分布不同，而较为平坦。但对于快中子来说，由于快中子速度较高，无论是瞬发中子或缓发中子，其等效吸收截面的绝对值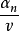都很小而可忽略。因而快中子的瞬发中子通量的空间分布和快中子的缓发中子通量的空间分布近似相同，它们都接近于静态的中子通量分布。在图4中列举了一个具有无穷水反射层的铀-水堆的热群瞬发中子通量的基波的空间分布与缓发中子通量的基波的空间分布的实测值与计算值的比较。从图中可以看出：越接近反射层，瞬发中子通量的分布与缓发中子通量的分布的差别越大，在反射层中二者有显著的差别。因而在反射层中或接近反射层处测得的结果需要进行动态畸变约修正2。

图4 有反射层的铀-水堆中的瞬发中子基波与缓发中子基波的空间分布

本词条内容贡献者为:

李雪梅 - 副教授 - 西南大学