[科普中国]-遭遇角

遭遇角在舵减摇控制中可通用线性模型与模糊线性模型的优缺点，采用了一种根据遭遇角的不同自动切换控制器设计模型的并行双模切换舵减摇控制方案。该方法辨识精度较高，且比传统重心法节省了在线计算量与存储数据库所需的存储空间，简化了辨识流程。

概念遭遇角是指船首前进的方向与波浪前进方向之间的夹角。遭遇角频率对船舶的航行安全和减摇效果都是至关重要的。然而，船舶操纵者无法直接预报出船舶的遭遇角频率，这对研究船舶在海浪中的运动造成了不便。为了解决上述问题，相关研究首先在特定海况下，通过海浪理论和Conolly理论建立海浪的波倾角模型和船舶的横摇运动模型，仿真出船舶的横摇历程，然后应用Welch谱估计方法估算船舶的横摇角谱，进而求取船舶发生最大谐振时的遭遇角频率，最后把估算出的遭遇角频率与理论上计算出来的船舶最大谐振的遭遇角频率进行比较分析，以验证该方法的有效性。

船舶遭遇角频率的估算船舶在海平面上行驶时，不可避免地会受到海洋环境的扰动使其运动姿态发生变化，其中在船舶遭受的所有扰动中，海浪对其造成的影响最大，由于船舶的遭遇角频率是船舶遭受到海浪的扰动后做出响应的频率，故它反应了船舶是如何遇上影响其运动的波浪的，因此估算遭遇角频率对研究船舶的运动姿态是非常有利的。

尚无直接预报船舶遭遇角频率的估计器，研究人员主要通过遭遇角与遭遇角频率之间的函数关系来间接地计算船舶在当前时刻的遭遇频率。而该方法存在的主要问题是海浪主浪向的计算较复杂。浪向的获取主要是借助于理论或者半经验海浪波谱、浮标、传感器阵列、波高仪阵列以及雷达卫星等方法。文献中都是通过船舶的运动获取海浪方向谱信息。文献1中也仅仅对单自由度二阶动力学系统研究船舶航行速度的变化引起遭遇频率的改变，以此建立了遭遇频率散射强度与摇荡的关系。以上方法需要的测量设备较多，计算量大。另外，鉴于工程应用的方便和海浪的复杂性，工程人员也常常把长峰波随机海浪设定为船舶的干扰信号，然而当船舶与海浪之间的遭遇角发生变化时，这种设定不能反应海浪的真实信息，从而会降低船舶的减摇效果。船舶运动信息是由船舶自身的特性和海浪环境的综合反映，同时也包含了遭遇角频率信息。基于上述原因，本文通过Welch谱估计方法估计船舶的横摇角谱，然后计算船舶在最大谐振时的遭遇角频率。

船舶横摇数据的获取由于测量实船的摇荡信息成本较高，周期较长，为了尽可能的减小船舶航行中信息采集的复杂性和代价，因此，在特定的海况条件下，我们根据平稳线性模型的假设，应用海浪线性叠加理论和MATLAB仿真软件生成所需要的船舶摇荡信息是一种比较经济、合理的方法。

谱估计对于一个随机信号，它本身的傅氏变换是不存在的，因此无法像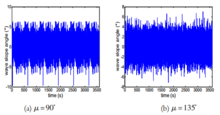确定性信号那样用数学表达式来精确地描述它，而只能用各种统计平均量来表征它。其中，自相关函数最能完整地表征它的特定统计平均量值。一个随机信号的功率谱密度正是自相关函数的傅里叶变换，我们可以用功率谱密度来表征它的统计平均谱特性。然而，实际应用中的平稳随机信号通常是有限长的，只能根据有限长的信号估计原信号的真实功率谱，所以，要在统计意义下描述一个随机信号，就需要估计它的功率谱密度（Power Spectral Density，简称PSD）。谱的估计方法可分为现代谱估计方法和经典谱估计方法。

仿真验证在特定海况下进行仿真，即设定海浪有义波高h1/3=3 m，特征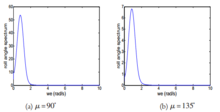周期T=8 s；船舶的航行速度V=18 kn=9.26 m/s。本文选用中国渔政船32号船的参数，将其代入计算出的船舶横摇运动的数学模型。由于论文要求的限制，本论文仅以遭遇角μ=90°、150°为例进行了仿真，仿真图形见图1至图2，其中所有(a)图对应遭遇角μ=90°时的仿真曲线，所有(b)图对应遭遇角μ=135°时的仿真曲线。

比较可知，遭遇角μ=90°时对船舶的影响比μ=150°时大，通过对图1和图2的对比计算，可以得到船舶遭遇角频率的理论值与估计值的对比表，见表1。

研究结论首先根据海浪理论和Conolly理论建立了海浪模型和船舶的横摇模型，然后对 Welch谱估计方法进行了理论推导，最后在特定的海况下进行了仿真验证。对仿真图形分析可知：在特定海况、定航速和不同遭遇角下，本文使用的Welch谱估计方法能较好地估算出船舶的遭遇频率，这为研究海浪与船舶的相互作用提供了有效的方法，为实现船舶减摇的变参数控制提供了可能，但其工程应用价值还有待于实船验证，本文还需对船舶在不同海况和不同航速下的情形做进一步的研究。2

基于遭遇角决策的并行双模切换舵减摇控制为减少风浪条件下舰船横摇对适航性产生的影响，人们不断地研究舰船减摇技术。舵减摇是一项新的减摇技术，具有减摇鳍不能替代的优点，如成本低、节省空间、不增加附体阻力、性价比高等，因此有着极其广阔的应用前景，在世界各国受到极大的关注。

由于横摇的动态受很多硬的和软的非线性因素的影响，因此舵减摇控制器的设计往往满足在某种特定范围内性能最优以在整个舰船可操范围内达到次优。文献采用某些鲁棒控制方法以考虑模型不确定性与非线性的影响，如 H∞，LQG与模型预测控制等。这些方法在某些海浪条件下取得的减摇效果一般，尤其是某些尾斜浪(遭遇角在30°～60°范围)时。究其原因，舰船运动在这些海浪条件下的非线性特性明显，采用通用线性模型设计的控制器控制性能要下降，而依据模糊线性模型设计的控制器仅仅适用于尾斜浪情况。因此，文中综合两种模型的优点，采用一种并行双模切换控制(parallel two mode switched control，PTMSC)方案，提出一种基于神经网络遭遇角的自动判断方法，并据判断结果完成控制器设计模型的决策。

并行双模转换控制方案为验证控制器性能而进行闭环系统仿真时，应使用非线性舰船模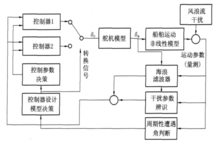型，以尽可能全面地描述原过程的动态特性。为避免过于复杂的非线性控制器设计过程，在保证和原过程特性大致相同的前提下建立一个较为适宜的线性模型。大多数舵减摇控制器设计主要采用的通用线性模型忽略了所有一阶以上或耦合的非线性项，故而此类控制器在舰船处于尾斜浪时的控制效果一般。作者另文简化出一种模糊线性模型，并基于此模型设计的控制器在尾斜浪情况下控制效果比较好，而在其它情况下可能由于模糊线性化的精度不高，其控制效果并不理想。因此，综合两种模型的优点，建立并行双模切换控制器，使其满足各种工况条件变化的方案需求。

PTMSC是由许多子系统与控制转换规则组成的混合系统，其结构如图3所示。它的控制策略分为高低两级，高级为根据环境进行的控制器设计模型决策与控制参数决策，低级为两类控制器。当海况与舰船航行速度相同时，控制器的设计主要依靠遭遇角来决策；当遭遇角相同、海况与航行速度不同时，则主要依靠控制参数来决策，如控制目标中的加权函数。

遭遇角自动判断众所周知，功率谱密度(power spectral density，PSD)是信号的功率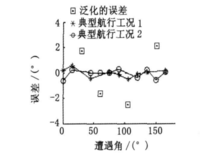在频域上的分布特性。试验证明，舰船航行速度与海况相同时，遭遇角不同，舰船横摇角的功率谱密度就不同。究其原因，遭遇角的改变引起横摇主导频率的改变，从而影响横摇角功率谱密度，因此通过对横摇PSD的分析来判断舰船遭遇角就成为可能。

三层神经网络可以实现任意复杂的非线性映射问题。因此，可采用单隐层的三层BP神经网络作为遭遇角自动判断模型。输入层为海浪有义波高、平均海浪周期、舰船航速；输出层为遭遇角。隐层神经元的数目往往与输入数据中隐含的特征因素有关，采用试凑法确定。隐层、输出层的激励函数均为线性函数。图4中仿真线型为两种典型航行工况、不同遭遇角时，采用动量梯度下降算法训练的单隐层BP神经网络的输出误差，方形点为泛化的误差，误差均在±3°以内，精度较高。训练完成后，神经网络固定，则可由现场采集数据，根据神经网络输出遭遇角供控制器设计模型决策使用。此方法中数据库数据的所有有用信息均包含于成功训练好的神经网络中，不必再储存数据库数据，节省了存储空间。且网络固定后，所有权值与阙值均固定，无需在线计算，节省了计算量。由于本方法无CFG法的匹配环节，因此简化了辨识流程。

研究结论综上所述，文中针对单一舰船舵减摇控制方法在舰船航行与海浪处于某些遭遇角时取得的减摇效果一般的问题，采用了并行双模切换控制方案。为在线自动辨识遭遇角，提出基于横摇功率谱密度柱状图的神经网络辨识方法。仿真结果表明：该方法辨识精度较高，且比传统重心法节省了在线计算量与需要存储数据库的存储空间，简化了辨识流程，具有较高的应用价值。3

本词条内容贡献者为:

张磊 - 副教授 - 西南大学