动态元件由于具有存储能量的作用,因此在电路的结构或元件的参数发生变化和换路时,其端电压和端电流是不能突然改变的。
在电路理论中这一性质可以表述为:当电容元件的初始电压为零或者电感元件的初始电流为零时,在换路的一瞬间,可以把电容元件看成一条短路线,把电感元件看成一个开路端。1
术语简介任何物理可实现电路,在换路瞬间电路中的储能不发生突变.
由于电容通过电场储能,能量公式为 0.5×C×sqrt(U)
所以在0+和0-这两个时间点的U必然是相等的,也即U不能突变(能量不能突变)。
同理,电感通过磁场储能,能量公式为 0.5×L×sqrt(I),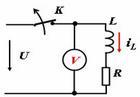 所以在0+和0-这两个时间点的I必然是相等的,也即I不能突变(能量不能突变)。
所以在0+和0-这两个时间点的I必然是相等的,也即I不能突变(能量不能突变)。
对于电容,U(0+)=U(0-),对于电感,I(0+)=I(0-)。就是换路定理的核心。
定理分析由动态元件组成的动态电路有一个重要的特征即:当电路的结构或元件的参数发生突然改变时(例如电路中电源的断开或接入、无源元件的断开或接入、元件参数的突然变化、信号的突然改变或置零等等),将会使电路改变原来的工作状态,转变到另外一种工作状态,这种情况称为“换路”, 而这种变化往往是和能量的变化连在一起的,而能量的变化是需要经历一个过程的,在工程上称为“过渡过程” 。
在求解“过渡过程”的变量时,必须有一个初始值的计算,例如动态元件中的电容元件(又称为储能元件),如果电路中仅含一个电容元件,该电路就称为一阶动态电路。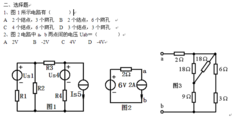
分析一阶动态电路的过渡过程方法之一仍然是根据KCL,KVL 和支路VCR 来建立描述电路的方程,该方程是以时间为自变量的线性微分方程,这种方法又称为经典法, 是一种在时间领域中分析的方法。
用经典法求解微分方程时,必须根据电路的初始条件确定解中的积分常数,而初始条件就是指电路中所求变量及其(n - 1)阶导数在t =0 +时的值, 这个值就称为初始值。
电容电压uC(0 +)称为独立的初始条件。
适用范围(1) 如果电路中存在有全部由电容元件组成的回路或由电容元件与理想电压源组成的回路,当激励接入或者换路时,电容电压可能发生跃变2。
(2)如果电路中存在有全部由含电感元件组成的割集或由含电感元件与理想电流源组成的割集,当激励接入或电路发生换路时,电感电流也可能发生跃变。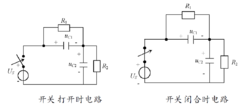
在电路发生“强迫跃变”的情况下,只能根据电荷守恒和磁链守恒的原理确定状态变量有关的初始值, 这时如果仍然按照“换路定理”进行分析与计算就是错误的。
与基尔霍夫定律的关系换路定理与基尔霍夫定律的关系换路定理的基本定义是”在换路前(t=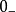 )和换路后(t=
)和换路后(t=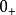 ),线圈的磁链不变[
),线圈的磁链不变[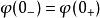 ],电容的电荷不变[
],电容的电荷不变[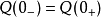 ]"。
]"。
因为如果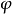 或
或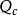 突变,则
突变,则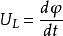 或
或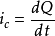 就会变成无穷大,这在电压源的电路中就要违背KVL,在电流源的电路中就要违背KCL。
就会变成无穷大,这在电压源的电路中就要违背KVL,在电流源的电路中就要违背KCL。
在线性(恒定参量)电路中,线圈的电感量L,电容的容量C 均为常数,这时因为 。, 便引伸出常用的衍定理,即:
。, 便引伸出常用的衍定理,即:
在换路前后, ,
,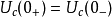 。
。
必须强调,衍定理的正确是有附带条件的, 即换路时原元件的参量L(或C) 不变。
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国