设交流量的函数式为:u=Umsin(ωt+φ),其中(ωt+φ)是一个角度,它是时间的函数,对所确定的时间t,有一个确定的角度。因此,(ωt+φ)是表示交流量在t时刻的角度,称为相位或相角。不同的相位对应着不同的瞬时值。通常把起始时的相位,即t=0时的相位叫做初相位或初相角,u=Umsin(ωt+φ)中,φ为初相位。两个频率相同的正弦量的相位之差叫做相位差,用△φ来表示。如两个同频率的正弦交流电压u1和u2,其函数式为:u1=Umsin(ωt+φ1),u2=Umsin(ωt+φ2),则它们之间的相位差△φ=(ωt+φ1)一(ωt+φ2)=φ1-φ2。由此可知,两个同频率的正弦交流电的相位差,就是初相位之差。
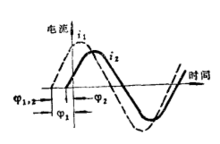
基本介绍如同时研究二个或多个周期变化的交变量,由幅值为零至某一瞬间值所占一个周期中的角度数,就称为相角。例如:甲交流量正在增大,但乙交流量却正在减少。如果取一瞬间来分析,则它们的瞬时值也许是不同的。如图:当时间是零时,电流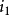 与电流
与电流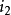 之瞬时值不同。为了说明这种现象,可用相位表示。电流
之瞬时值不同。为了说明这种现象,可用相位表示。电流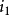 在循环刚开始时(或者说
在循环刚开始时(或者说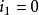 的时间),与我们研究的某一瞬间(t=0的时间)相差多少,以角度表示,即为此
的时间),与我们研究的某一瞬间(t=0的时间)相差多少,以角度表示,即为此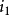 的初相角。一个周期相当于360°角(即
的初相角。一个周期相当于360°角(即 角)。如图,
角)。如图,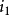 之初相角是
之初相角是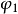 ,
,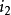 之初相角是
之初相角是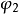 。但如果我们研究的瞬间改为刚好是
。但如果我们研究的瞬间改为刚好是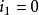 时,则
时,则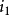 之初相角是零,但
之初相角是零,但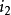 之初相角则为
之初相角则为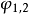 。所以初相角是相对的,比较的,用它可以说明若干个交流量的循环起始位置。
。所以初相角是相对的,比较的,用它可以说明若干个交流量的循环起始位置。
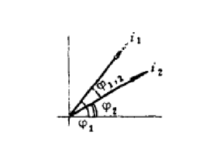
初相角又可用矢量表示,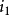 与横轴所夹的角为
与横轴所夹的角为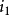 之初相角
之初相角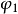 ,
,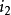 与横轴所夹的角为
与横轴所夹的角为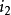 之初相角
之初相角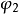 。
。
注意点(1)初相角通常是在180°的范围内取值,相位差也在该范围内取值。初相角用角度或弧度表示均可。
(2)凡是同频率的任意两个正弦量,不管是两个电压还是两个电流,或者是一个电压一个电流,都可以讨论它们的相位关系。频率不同的两个正弦量,因它们没有确定的相位差,所以讨论它们之间的相位差是没意义的。
(3)相位差与计时起点的选择无关。因为当两个同频率正弦量的计时起点改变时,它们的初相角也随之改变。但两者的相位差仍保持不变。
相关概念相位差两个正弦交流电它们的振幅和角频率完全相同,但是初相角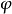 不同,我们不能说这两个正弦交流电完全相同。正弦交流电的初相角不相同,反映两个正弦交流电在相位上的不同,初相角对分析正弦交流电是非常重要的。如果两个振幅和频率相同的正弦交流电流初相角也相同,则两电流相加振幅增大一倍,如果初相角相差
不同,我们不能说这两个正弦交流电完全相同。正弦交流电的初相角不相同,反映两个正弦交流电在相位上的不同,初相角对分析正弦交流电是非常重要的。如果两个振幅和频率相同的正弦交流电流初相角也相同,则两电流相加振幅增大一倍,如果初相角相差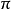 ,则两电流完全反相,相加后互相抵消,合成电流为零。
,则两电流完全反相,相加后互相抵消,合成电流为零。
初相角是指在t=0时的正弦交流电的相位角,两个不同初相角的交流电流可以表示为:
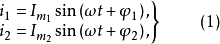
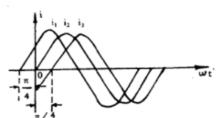
实际上初相角与时间的起点选择有关,时间起点不同初相角也不同。t=0时,函数值为零,则初相角为零;函数值为正,初相角为正;函数值为负,初相角为负。图3表示三种不同初相角的交流电流,其中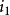 的初相角为
的初相角为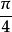 ,
,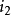 的初相角为零,
的初相角为零, 的初相角为
的初相角为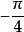 ,它们的瞬时值分别为:
,它们的瞬时值分别为:
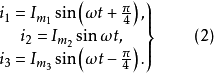
习惯上初相角不用大于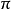 的角来表示,当初相角大于
的角来表示,当初相角大于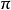 时可化成小于
时可化成小于 的负角表示。例如超前号
的负角表示。例如超前号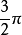 可用
可用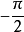 来表示。
来表示。
为了比较两个同频率的正弦交流电的相位关系,引入相位差的概念。两个同频率的正弦交流电相位之差叫做相位差。式(1)中的两个电流相位差为:
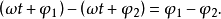
这说明两个同频正弦交流电的相位差等于它们初相角之差,而与角频率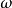 及时间
及时间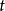 没有关系,通常把初相角为零的正弦量叫做参考正弦量。在图3中,
没有关系,通常把初相角为零的正弦量叫做参考正弦量。在图3中,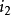 为参考正弦电流,
为参考正弦电流,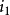 比
比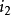 的相位超前
的相位超前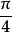 ,
, 比
比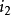 的相位落后
的相位落后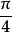 ,因此
,因此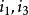 与参考电流
与参考电流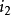 的相位差分别为
的相位差分别为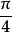 和
和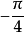 ,而
,而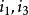 之间的相位差为
之间的相位差为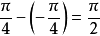 。
。
实际上,参考正弦量的选择是任意的。例如在图1中,选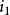 为参考电流,则
为参考电流,则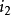 比
比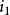 落后
落后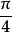 ,
, 比
比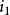 落后
落后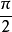 。它们之间的相位差不因参考电流的改变而变化。
。它们之间的相位差不因参考电流的改变而变化。
相位差与交流量的关系从以上讨论可以看出,相位差实际上说明两个正弦量在时间上的超前或滞后的关系。如果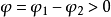 ,则说明
,则说明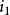 超前
超前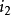 ,即
,即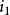 的最大值出现时刻比
的最大值出现时刻比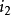 早φ,如果
早φ,如果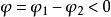 ,则说明
,则说明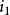 滞后
滞后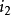 ,电流
,电流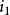 的最大值出现比
的最大值出现比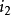 滞后一个φ角。
滞后一个φ角。
相位差为零的两个正弦交流电称为同相,相位差为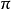 的两个正弦交流电称为反相,相位差为
的两个正弦交流电称为反相,相位差为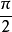 的两个正弦交流电称为正交1。
的两个正弦交流电称为正交1。
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国