一般指含有某些三角函数的方程,这些三角函数的自变量中含有未知数,含有未知数的三角函数的方程叫做三角方程。
适合于方程的一个未知数的实数值(可以理解为角的弧度数)叫做三角方程的一个解;适合于方程的未知数的实数值的集合叫做三角方程的通解。
定义一般指含有某些三角函数的方程,这些三角函数的自变量中含有未知数,含有未知数的三角函数的方程叫做三角方程。1
三角方程是三角中的重要内容,在解三角方程过程中,运用的知识比较广泛,不仅要用到三角中的许多定理与公式,还要涉及代数式的变形与代数方程等代数知识,最简单的三角方程实际上是由某角的三角函数值求角问题的延伸,是三角函数的周期性和反三角函数概念的最直接运用。
目前高中数学教材已经删除相关内容。
解题方法套用通解公式把一般的三角方程转化为最简单的三角方程,其中要应用到三角函数性质及图像、反三角函数、诱导公式等知识。
一是要掌握其基本方法,要熟悉同名三角函数相等时角度之间的关系在解三角方程中的作用;会用数形结合的思想和 函数思想进行含有参数的三角方程的解的情况和讨论。通过解三角方程,可以进一步理解三角函数及反三角函数,进一步提高三角变换能力。
二是要合理选用公式和变换方法。
基本转化方法(1)化为同角、同名的三角函数;
(2) 因式分解法;
(3)化为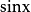 和
和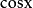 齐次方程求解;
齐次方程求解;
(4)引入辅助角;
(5)利用三角函数定义求解;
(6)利用比例性质;
(7)利用升降次法;
(8)利用 换元法;
(9)利用万能置换法。
通过解三角方程,进一步理解三角函数及反三角函数,进一步提高三角变换能力。1
基本三角方程的通解1.若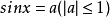 , 则
, 则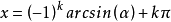
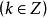 .
.
2.若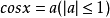 ,则
,则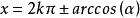
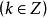 .
.
3.若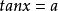 ,则
,则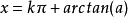
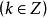 .
.
4.若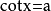 ,则
,则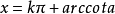
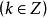 .
.
5.要使方程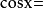
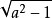 有解,则a的取值范围是
有解,则a的取值范围是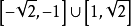 .
.
6.方程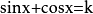 在
在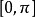 上有两解,则k的取值范围是
上有两解,则k的取值范围是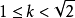 .
.
三角方程举例形如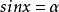 的方程叫做最简三角方程。
的方程叫做最简三角方程。
解三角方程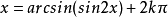
首先,明确一下反正弦函数: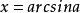 表示一个在[-π/2,π/2]范围内的角,且其正弦值为a(a在[-1,1]),即sinx=a
表示一个在[-π/2,π/2]范围内的角,且其正弦值为a(a在[-1,1]),即sinx=a
解:由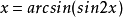 ,知-π/2
,知-π/2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国