[科普中国]-分布曲线

分布曲线是以变数值为横坐标，以累积频率[概率]为纵坐标的曲线图，即概率分布函数的图形。例如正态曲线等。

概念分布曲线是以变数值为横坐标，以累积频率[概率]为纵坐标的曲线图，即概率分布函数的图形。例如正态曲线等。1

分布曲线使标准分数在实际运用时非常有用。知道了Z分数，就能立刻知道该分数是在均数以上还是在均数以下。又因为标准分数是根据标准差求得的，知道了标准分数也就知道了它出现的概率。比如，在整个常态分布中，有34%的分数位于从均数到1个标准差的区域内（0≤|Z|≤1），16%的分数位于分布的两端超出1个标准差的区域（|Z|>1），大于2个标准差的分数只占2。5%（|Z|>2）。

表示一个人的的得分在一个团体中的相对地位，可以在使用百分等级之外，选择使用〝标准分数〞：Z分数和T分数。

也就是将原始分数转换为一种以平均数为基准，以标准差为单位的距变数。以标准分数的优点来说：可以直接比较某生在不同考试中的相对地位或不同考生在不同考试中的相对地位。

正态分布分布曲线一种概率分布。正态分布是具有两个参数μ和σ2的连续型随机变量的分布，第一参数μ是遵从正态分布的随机变量的均值，第二个参数σ2是此随机变量的方差，所以正态分布记作N(μ，σ2)。遵从正态分布的随机变量的概率规律为取μ邻近的值的概率大，而取离μ越远的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。正态分布的密度函数的特点是：关于μ对称，在μ处达到最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点。它的形状是中间高两边低，图像是一条位于x轴上方的钟形曲线。当μ=0，σ2=1时，称为标准正态分布，记为N（0，1）。μ维随机向量具有类似的概率规律时，称此随机向量遵从多维正态分布。多元正态分布有很好的性质，例如，多元正态分布的边缘分布仍为正态分布，它经任何线性变换得到的随机向量仍为多维正态分布，特别它的线性组合为一元正态分布。

正态分布最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。

生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。例如，在生产条件不变的情况下，产品的强力、抗压强度、口径、长度等指标；同一种生物体的身长、体重等指标；同一种种子的重量；测量同一物体的误差；弹着点沿某一方向的偏差；某个地区的年降水量；以及理想气体分子的速度分量，等等。一般来说，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个量具有正态分布（见中心极限定理）。从理论上看，正态分布具有很多良好的性质，许多概率分布可以用它来近似；还有一些常用的概率分布是由它直接导出的，例如对数正态分布、t分布、F分布等。

正态分布应用最广泛的连续概率分布，其特征是“钟”形曲线。

概率分布概率分布，是概率论的基本概念之一，主要用以表述随机变量取值的概率规律。为了使用的方便，根据随机变量所属类型的不同，概率分布取不同的表现形式。事件的概率表示了一次试验某一个结果发生的可能性大小。若要全面了解试验，则必须知道试验的全部可能结果及各种可能结果发生的概率，即必须知道随机试验的概率分布。

概率分布律[law of probability distribution]简称概率律或概率分布。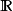上描述随机变量取值规律的概率测度。假定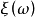是概率空间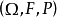上的随机变量则由

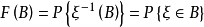所定义的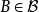上的集函数 F 是一个概率测度，称为随机交量的概率分布律。对于任何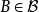随机变量落入B中的概率可通过计算B 的测度F(B) 得出这就是说概率分布F 完全刻画了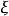取值的概率规律。2

概率密度概率指事件随机发生的机率，对于均匀分布函数，概率密度等于一段区间(事件的取值范围)的概率除以该段区间的长度，它的值是非负的，可以很大也可以很小。

对于随机变量X的分布函数F（x），如果存在非负可积函数f(x)，使得对任意实数x，有

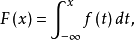
则X为连续型随机变量，称f(x)为X的概率密度函数，简称为概率密度。

单纯的讲概率密度没有实际的意义，它必须有确定的有界区间为前提。可以把概率密度看成是纵坐标，区间看成是横坐标，概率密度对区间的积分就是面积，而这个面积就是事件在这个区间发生的概率，所有面积的和为1。所以单独分析一个点的概率密度是没有任何意义的，它必须要有区间作为参考和对比。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学