[科普中国]-策略迭代法

策略迭代法（policy iteration method）是动态规划中求最优策略的基本方法之一。它借助于动态规划基本方程，交替使用“求值计算”和“策略改进”两个步骤，求出逐次改进的、最终达到或收敛于最优策略的策略序列。

计算例如，在最短路径问题中，设给定M个点1，2，…，M。点M是目的点，сij>0是点i到点j的距离i≠j，сij=0，i,j=1,2,…,M,要求出点i到点M的最短路。记ƒ(i)为从i到M的最短路长度。此问题的动态规划基本方程为：

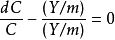其策略迭代法的程序如下：选定一初始策略u0(i)，在这问题中，策略u(i)的意义是从点i出发走一步后到达的点，而且作为策略，它是集{1,2,…,M-1}上的函数。由u0(i)解下列方程组求出相应的值函数ƒ0(i)：

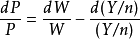再由ƒ0(i)求改进的一次迭代策略u1(i)，使它是下列最小值问题的解：

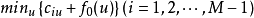然后，再如前面一样，由u1(i)求出相应的值函数ƒ1(i)，并由ƒ1(i)求得改进的二次迭代策略u2(i)，如此继续下去。

步骤可见求解(1)的策略迭代法的程序由下列两个基本步骤组成：

①求值计算 由策略 un(i)求相应的值函数ƒn(i)，即求下列方程的解：

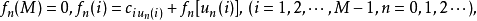②策略改进 由值函数ƒn(i)求改进的策略，即求下列最小值问题的解：

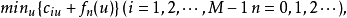式中规定，如un(i)是上一问题的解，则取un+1(i)=un(i)。

在一定条件下，由任选的初始策略出发，轮换进行这两个步骤, 经有限步N后将得出对所有i，uN+1(i)=uN(i)这样求得的uN(i)就是最优策略，相应的值函数ƒN(i)。是方程(1)的解。

对于更一般形式的动态规划基本方程

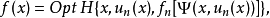
这里ƒ，H，φ为给定实函数。上述两个步骤变成：

①求值计算 由策略un(x)求相应的值函数 ƒn(x)，即求方程 之解，n=0，1，2…。

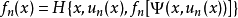
②策略改进 由值函数ƒn(x)求改进的策略un+1(x)，即求最优值问题（图8）的解。

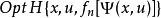对于满足适当条件的方程(2)和初始策略，上述两个步骤的解存在，并且在一定条件下，当n→ 时，所得序列{ƒn(x)}与{un(x)}在某种意义下分别收敛于(2)的解和最优策略。

策略迭代法最初是由R.贝尔曼提出的。1960年，R.A.霍华德对于一种马尔可夫决策过程模型，提出了适用的策略迭代法，给出了相应的收敛性证明。后来，发现策略迭代法和牛顿迭代法在一定条件下的等价性，于是，从算子方程的牛顿逼近法的角度去研究策略迭代法，得到了发展。

对于范围很广的一类马尔可夫决策过程，其动态规划基本方程可以写成

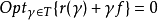式中ƒ∈V，对所有 γ∈Γ:r(γ)∈V，γ为 V→V的线性算子，Γ为这种算子的族，而V 则是由指标值函数所构造的函数空间。

假设 当 ƒ(γ)是方程 r(γ)+γƒ=0 的解时，它是对应于策略γ的指标值函数。

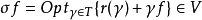最优策略，定义为最优值问题的解。

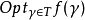这时由策略迭代法所求得的序列{fn}和{γn}满足下列关系 ，其中的逆算子。1

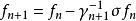当σ是加托可微时, γn+1是σ在ƒn处的加托导数。于是，上面的关系恰好表达了牛顿迭代法在算子方程中的推广。

解决问题利用迭代算法解决问题，需要做好以下三个方面的工作：

一、确定迭代变量。在可以用迭代算法解决的问题中，至少存在一个直接或间接地不断由旧值递推出新值的变量，这个变量就是迭代变量。

二、建立迭代关系式。所谓迭代关系式，指如何从变量的前一个值推出其下一个值的公式（或关系）。迭代关系式的建立是解决迭代问题的关键，通常可以使用递推或倒推的方法来完成。

三、对迭代过程进行控制。在什么时候结束迭代过程？这是编写迭代程序必须考虑的问题。不能让迭代过程无休止地重复执行下去。迭代过程的控制通常可分为两种情况：一种是所需的迭代次数是个确定的值，可以计算出来；另一种是所需的迭代次数无法确定。对于前一种情况，可以构建一个固定次数的循环来实现对迭代过程的控制；对于后一种情况，需要进一步分析出用来结束迭代过程的条件。

动态规划动态规划是旦泽和贝尔曼提出的，他们关于这一定量化方法的重要著作发表于50年代。最初动态规划指的是不确定性的线性规划问题，而现在它已发展成为一个解决范围广泛的工商业务问题的定量技术了。

动态规划的理论基础为“最优化原则”。它是说一个最优策略是由最优子策略构成的。它可以定义为这样的一个数学方法：它解决一串序贯决策问题，而这些决策中的每一个都又影响着未来的决策，且后面的决策对前面决策所决定的初始状态来说总是最优的。这是非常重要的，因为我们很难遇到一个运行中的情况；其中的决策不影响未来的决策。经理们面对着的问题是要他们作出一系列决策，这些决策中的每一个都依赖于先前决策的结果。例如，一个生产经理可能为了得到眼前的高产量不顾未来的高产量而忽视工厂的维修工作。若每一决策只考虑它本身最优化，那么由全部决策所得到的收益可能不是最优的。相反如果在制定第1个或后续的决策时在收益上作些牺牲，虽然使各决策次优化了，但总的收益可能更高些。这就是动态规划的目标。

一般说来，动态规划处理的问题都含有时间变量。但是，它可以用来处理一些本来与时间无关的问题，这只要在静态模型中人为地引进“时间”因素，分成时段，把它看作多阶段的动态模型就能用动态规划的方法来解决了。

在很多领域中都有动态规划的应用。如资源分配、货物装运、设备更新、生产计划和存贮、排序、确定利息策略及评价投资机会等。

动态规划可以看成是一个把复杂的大问题分成一系列较易解决的小问题的方法。它没有标准的格式。

动态规划模型有4个基本概念：(1)阶段。它是所给问题中被划分成若干个相互联系的时期或区间。(2)状态变量。是表示某段的出发位置。这些状态变量的值把制定决策需要了解的所有有关系统的情况都显示出来。状态变量数目可能很大，对于一定的计算能力，应尽能减少状态变量的数目。(3)决策变量。表示状态给定以后，从该状态到下一阶段某状态的选择。(4)目标函数。各个不同阶段的决策能力，可能是距离、利润、成本等。2

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学