[科普中国]-反演变换

设在平面内给定一点O和常数k（k不等于零），对于平面内任意一点A，确定A′，使A′在直线OA上一点，并且有向线段OA与OA′满足OA·OA′=k，我们称这种变换是以O为的反演中心，以k为反演幂的反演变换，简称反演。称A′为A关于O（r）的互为反演点。

当k>0时，有向线段OA与OA′同向，A与A′在反演极同侧，这种反演变换称为正幂反演，亦叫双曲线式反演变换。

当k0，作点A的反演点A′。

令k=r^2，作出反演基圆⊙O（r），

1）若点A在⊙O（r）外，则过点A作圆的切线(两条),两个切点相连与OA连线交点就是点A′。

2）若点A在⊙O（r）内，则把上述过程逆过来：连结OA，过点A作直线垂直于OA，直线与⊙O（r）的交点处的切线的交点就是点A′。

3）若点A在⊙O（r）上，反演点A′就是点A自身。

圆的反演变换性质1.除反演中心外，平面上的每一个点都只有唯一的反演点，且这种关系是对称的，位于反演圆上的点，保持在原处，位于反演圆外部的点，变为圆内部的点，位于反演圆内部的点，变为圆外部的点。 举个最简单的例子，区间(0,1]以1为反演半径，那么反演后的区间就是[1,+∞)，这就是一维反演，而圆的反演是二维反演。

2.任意一条不过反演中心的直线，它的反形是经过反演中心的圆，反之亦然，特别地，过反演中心相交的圆，变为不过反演中心的相交直线2。

画图1.首先约定，反演圆的圆心O是反演中心。规定反演半径就是反演圆的半径r（在解题和具体的应用上，可以用不同的反演半径，不必非得是反演圆的半径）。再约定，如果A经过反演之后变成A'，那么，O、A、A'共线，且OA·OA'=r^2。 具体的作图过程，见下面的图1。注意，要把反演点视为圆和直线的交点，而不是圆和线段的交点，因为反演点有可能跑到线段的延长线上，此时几何画板有可能忽略这些点。

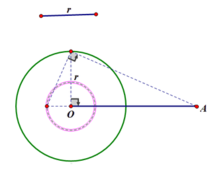
2.不同的图形会有不同的反演成像。同一个图形，如果到反演中心的距离不同，也会有不同的反演成像。下面，就用几何画板演示一个几何图形的反演成像。在几何图形上取任意点P，作出它的反演点P'，选中P、P'，构造轨迹，这时候看到P'的轨迹就是反演成像。这时候，改变原图与O的距离，看看成像会有什么变化。

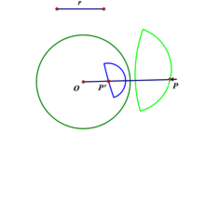
3.圆在不同情形下的反演成像。

当圆不经过反演中心，它的反演图形仍旧是个圆：

当圆与反演圆相交，交点是保持不变的；

当圆在反演圆的外面的时候，反演成像位于圆的内部；反过来，当圆位于反演圆的内部，反演成像位于圆的外部。

当圆经过反演中心，它的反演图形是一条直线。

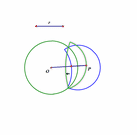
作点的反演变换，是一个繁琐的过程，尤其是要作多个图形的反演变换，只能一步一步地作出各个图形的反演图形。怎么快速作多个图形的反演变换呢？只能用自定义工具了。我们先把“点的反演变换”作成一个工具，可以快速地作出曲线上自由点的反演点，然后构造轨迹，就画出了曲线的反演图形。

具体的步骤如下：

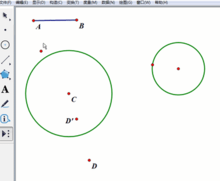
打开几何画板，新建文件，在画布上绘制四个点A、B、C、D；

连结线段AB，以C为圆心、AB为半径作圆（这就是反演圆，AB为反演半径）；

作出D的反演点D'。

用反演变换的方法来构造Steiner圆链。这里用一个简单的情形来演示一下：

先作一个圆及其内接正六边形，连结圆心和正六边形的顶点，把正六边形分成六个小三角形；

作出这六个小三角形的内切圆，可以知道这六个小圆是依次相切的；

隐藏各直线型和大圆，但保留大圆圆心；

作大圆的两个同心圆，分别与六个小圆相外切、相内切；

对这整个图形作反演变换，反演变换的结果是，同心圆变成偏心圆。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学