极限论有多个指代意义。一是作为微积分的基础,高等数学研究的主要内容是函数的微积分,微积分是研究函数的行为、性质和应用的数学学科,它的基本内容为:极限论、微分学和积分学,微分学研究函数的局部性质,积分学研究函数的全局性质,而极限论是整个微积分的基础1。极限论还指“增长极限论”,关于世界经济增长受环境制约最终将被迫停止的理论观点。由美国学者米都斯(D.H.Meadows)等人受罗马俱乐部委托后经研究提出。全部内容见《增长的极限》。
微积分的极限论基本介绍极限论是数学分析的基础,它研究极限的性质及极限存在的条件,建立求极限的法则,通过这些法则能够利用某些简单的变量的极限求出这些量的简单函数的极限。
极限论的基础是无穷小量的概念,也就是极限为0的变量,变量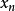 以常数
以常数 为其极限的充要条件是差
为其极限的充要条件是差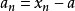 是无穷小量,若变虽
是无穷小量,若变虽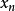 趋向于极限a且
趋向于极限a且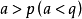 ,则从某一种时刻起, 其所有值都大于p(小于q),变量
,则从某一种时刻起, 其所有值都大于p(小于q),变量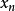 不能同时有两个不同的极限。
不能同时有两个不同的极限。
极限论中有一系列关于简化求极限过程的定理。若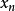 和
和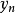 对于所有的n都有
对于所有的n都有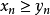 ,而
,而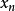 和
和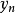 都有有穷极限
都有有穷极限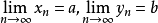 ,则a≥b。若
,则a≥b。若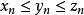 ,且存在极限
,且存在极限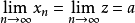 ,则
,则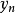 亦有相同的极限,即
亦有相同的极限,即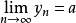 。
。
对于变量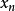 可以实行算术四则运算,若存在有穷极限
可以实行算术四则运算,若存在有穷极限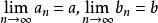 (且b≠0),则存在有穷极限
(且b≠0),则存在有穷极限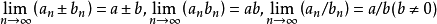 。若
。若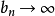 或
或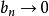 , 则分别有
, 则分别有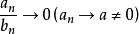 和
和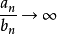 ,若两序列同时趋向于0或
,若两序列同时趋向于0或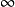 ,则分别称
,则分别称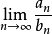 为不定型
为不定型 和
和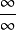 ,要确定不定型,也就是确定
,要确定不定型,也就是确定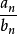 的极限,可以采用不同的方法,最一般而简便的方法是洛必大法则。
的极限,可以采用不同的方法,最一般而简便的方法是洛必大法则。
若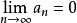 ,而
,而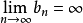 ,则
,则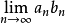 是
是 型不定型,若
型不定型,若 ,则其差的极限
,则其差的极限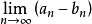 叫做
叫做 型不定型。
型不定型。
极限论还建立了极限存在准则(收敛准则),若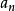 单调不减
单调不减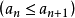 ,并有上界
,并有上界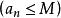 ,则
,则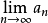 存在(若
存在(若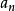 无上界,则当
无上界,则当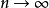 时
时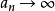 ),对于单调不增而有下界的序列亦有类似结论。在一般情况下,序列xn有有穷极限的充要条件是对于任意小的ε>0,存在着正整数N,当n>N,n'>N时,不等式
),对于单调不增而有下界的序列亦有类似结论。在一般情况下,序列xn有有穷极限的充要条件是对于任意小的ε>0,存在着正整数N,当n>N,n'>N时,不等式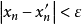 成立(柯西-波尔查诺定理),换句话说, 当变量xn的角码增大时,其值就彼此无限地接近起来。
成立(柯西-波尔查诺定理),换句话说, 当变量xn的角码增大时,其值就彼此无限地接近起来。
在极限论中还研究序列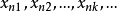 ,其中各项是从已知的xn中取出的, nk——递增的某自然数序列:
,其中各项是从已知的xn中取出的, nk——递增的某自然数序列: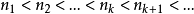 这里取所有自然数值的角码已不是n, 而是k;当
这里取所有自然数值的角码已不是n, 而是k;当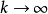 时,
时,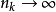 ,这个序列
,这个序列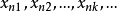 叫做部分序列。
叫做部分序列。
若原序列有极限,则其部分序列亦有相同的极限,对于任一有界序列总可以找出具有有穷极限的部分序列(波尔查诺-维尔斯特拉斯原理),这个极限称为已知序列的部分极限(或聚点),总存在有最大的部分极限(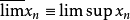 和最小的部分极限(
和最小的部分极限( ),若
),若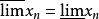 ,则xn有极限(通常意义下的极限),它们的相同的值就是极限值。
,则xn有极限(通常意义下的极限),它们的相同的值就是极限值。
上述关于变量xn(数值序列)的所有基本概念都可以推广到函数上去。当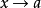 时
时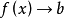 的充要条件是:对于以a为极限的任一数值序列
的充要条件是:对于以a为极限的任一数值序列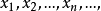 ,所对应的函数值序列,即数值序列
,所对应的函数值序列,即数值序列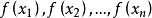 ,…有其自己的极限b。
,…有其自己的极限b。
古希腊的学者们曾运用极限过程求各种图形的面积,虽然那时还没有“极限”这个术语,极限论是17世纪开始建立的,符号lim是牛顿引入的(1686),他为了流数方法而发展了极限论,单调序列极限的概念是由法国数学家达兰贝尔建立的,近代极限论是建立在波尔查诺-柯西准则(1817)基础上的,现代的极限的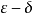 定义是由德国数学家维尔斯特拉斯给出的(1880)2。
定义是由德国数学家维尔斯特拉斯给出的(1880)2。
微积分概念的基本原理属于无穷小问题,但并非“无穷小”世界的全部,如果已经认清了无穷小,自然对建立微积分游刃有余,反之,若仅从微积分概念的需要出发,则并不需要完全地认清“无穷小”,只需极限论即可。
亦即无穷小认识对于建立微积分的需要来说是充分的,但并非必要,当然,这点只是个认识性结论,仅是建立在实际观察基础上的,并没有严格的逻辑证明,事实上,从当初极限论的诞生能折服整个科学界这点,加上逾一个世纪的科学实践检验,我们有理由相信,它对于微积分学的基础来说已是足够的,因此单纯从微积分角度说,极限论应该是值得肯定的。
但我们这里是以完全地认识“无穷小世界”为目标,那么,在此标准下即可发现,极限论是不能代替无穷小认识的,因而相对来说,它是有缺陷的。
极限论的优越性1.极限论给出了又一种用有限去表述无穷的方法
周期是自然界广泛存在的一种典型的用来表现无穷的有限形式,因此其理论也十分重要且广泛。那么,极限论包括无穷级数形式研究可算是另一种用有限来表征无穷的形式,甚至还是用以获得无穷结论的手段。这是十分了不起的。
2.极限论带来了微积分方法的“算术化”
由于极限的(公理化)定义来得简练而确切,致使由它建立起来的微分、积分定义也来得简练明快,没有繁复之感,以致整个微积分方法之容易掌握和运用,被科技界公认为“算术化”了的方法,它完全可以被列为算术第九则、十则运算,归根结底这是极限概念之简练性获得的效果。
3.极限论在微积分学上的实用效果是成功的
因为百余年来甚至说300余年来对微积分学激烈的研究,已经是对极限定义的一个严格检验过程。或可以说,几百年来,微积分学已被研究得相当成熟,尽管今天在初等微积分范围内还有论文,但已看不到突破性、基础性成果了,一个学科能达到这种状态已算是成熟的了,但是,却一直未发现在微积分意义下极限概念有什么不足。
不过必须指出,只能说是从微积分学来讲,极限论是成功的、完备的,不过将看到,若超出微积分概念,直接针对无穷小的认识,极限概念则显得远远不足了3。
增长极限论增长极限论又称“零增长理论”、“经济增长有限论”。是1972年由美国学者梅多斯(D.L.Mea-dows)等人在为罗马俱乐部所写的名为《增长的极限》的报告中对经济增长提出的一种观点。罗马俱乐部是1968年4月由知名科学家、经济学家、社会学家等组成的一个研究团体,旨在研究资源、环境、人口等“人类困境”问题。第二次世界大战后,西方主要资本主义国家运用凯恩斯经济理论,实施国家干预主义政策,在使经济出现持续、高速增长的同时,也带来了资源的迅速消耗及生存环境的恶化。该报告认为:工业化的结果必然造成对自然和生态的极度破坏。只有当人口和工业投资都停止增长时,才能在世界范围内实现真正的经济均衡。他们把经济增长所带来的各种矛盾和问题归结为相互影响的五种因素,即人口增长、农业生产、资源消耗、工业投资和环境污染。根据当时的资源条件和发展速度,这五种因素都呈指数增长,因此是难以为继的。他们综合考察这五种因素,并编成一组全球模型进行模拟计算,得到的结果是:1970年以后,人口和工业仍维持着指数增长,但迅速减少的资源将限制这种增长。工业化达到最高点后,人口和环境污染还会继续增长;但由于粮食缺乏、环境污染,最后人口也将停止增长。预计2100年到来之前,全球就会停止增长,社会因此而崩溃。其结论是,为避免此类情形的发生,必须在1975年之前停止人口增长,1990年之前停止工业投资增长,以达到零增长的全球性均衡状态。他们归纳的使人口和工业投资都停止增长的办法是:(1) 每年的人口出生率应等于预计的死亡率,(2) 每年的投资率应等于折旧率。零增长理论提醒人们必须关注经济增长与环境污染、资源利用、世界人口增长等问题的相互关系,综合考虑各种因素的影响。当然,这只是一种警示性的理论,其结论也过于消极悲观4。
极限论的思想方法同于生态学中的 “环境容量” 概念。环境容量是指生物种群增长的上限,达到上限时种群停止增长。米都斯等人认为社会经济发展也有类似的规律。所谓 《增长的极限》,实指社会经济发展的环境容量。极限论虽然深刻地揭示了经济增长同环境的对立关系,但否认科学技术和经济发展的调节机制可以改变环境限度;虽然正确地看到地球环境容量是人口和经济增长的限制因素,但没有看到这种限制因素是促进人类开发新资源、新技术和改进经济模式、改革社会关系的强制性推动力量,没有看到人与环境的冲突也是人类社会发展的动力之一 。极限论是悲观主义的环境理论5。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国