拉格朗日中值定理又称拉氏定理,是微分学中的基本定理之一,它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形,是泰勒公式的弱形式(一阶展开)。
法国数学家拉格朗日于1797年在其著作《解析函数论》的第六章提出了该定理,并进行了初步证明,因此人们将该定理命名为拉格朗日中值定理。1
定律定义定理表述如果函数f(x)满足:
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导;
那么在开区间(a,b)内至少有一点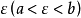 使等式
使等式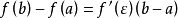 成立。
成立。
其他形式记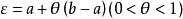 ,令
,令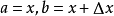 ,则有
,则有
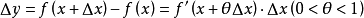
上式称为有限增量公式。2
在学习微分的时候,我们知道函数的微分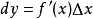 是函数的增量Δy的近似表达式,一般情况下只有当|Δx|很小的时候,dy和Δy之间的近似度才会提高;而有限增量公式却给出了当自变量x取得有限增量Δx(|Δx|不一定很小)时,函数增量Δy的准确表达式,这就是该公式的价值所在。
是函数的增量Δy的近似表达式,一般情况下只有当|Δx|很小的时候,dy和Δy之间的近似度才会提高;而有限增量公式却给出了当自变量x取得有限增量Δx(|Δx|不一定很小)时,函数增量Δy的准确表达式,这就是该公式的价值所在。
验证推导辅助函数法:
已知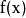 在
在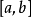 上连续,在开区间
上连续,在开区间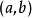 内可导,
内可导,
构造辅助函数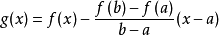
可得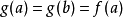
又因为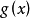 在
在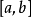 上连续,在开区间
上连续,在开区间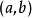 内可导,
内可导,
所以根据罗尔定理可得必有一点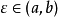 使得
使得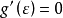
由此可得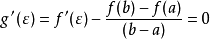
变形得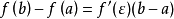
定理证毕。
定理推广推论如果函数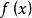 在区间
在区间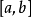 上的导数
上的导数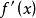 恒为零,那么函数
恒为零,那么函数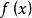 在区间
在区间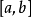 上是一个常数。
上是一个常数。
证明在区间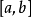 上任取两点
上任取两点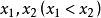 由拉格朗日中值定理得
由拉格朗日中值定理得
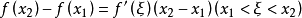
由于已知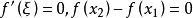 即
即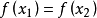
因为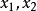 是区间
是区间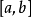 上的任意两点,所以
上的任意两点,所以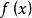 在区间
在区间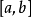 上的函数值总是相等的,
上的函数值总是相等的,
即函数在区间上是一个常数。
推广如果函数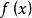 在开区间
在开区间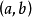 内可导且
内可导且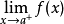 与
与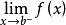 都存在
都存在
令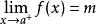 ,
,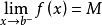
则在开区间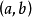 内至少存在一点
内至少存在一点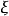 使得
使得
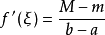
拉格朗日中值定理中的θ拉格朗日中值定理有一个变形,即所谓的有限增量公式:f(x0+Δx)-f(x0)=f'(x0+θΔx)Δx,0




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国