[科普中国]-拓扑指数

拓扑指数（topological index）是分子结构数值化的一种方式，它通过对表征分子图的矩阵实施某种数字运算而获得，是一种图的不变量，直接产生于分子结构，反映了化合物的结构特征。应用比较广泛的有4 种拓扑指数：分子连接性指数、电拓扑状态指数、分子电性矩矢量及Kappa 指数。

简介拓扑指数是分子结构的数学描述符，用以反映分子的大小、形状、分支等结构特征，从而实现分子结构信息的数值化。由于分子拓扑指数计算简便、取值客观且不受经验和实验的限制，因此应用非常广泛，已有200 多种不同类型的拓扑指数被提出。利用拓扑指数与化合物的理化性质、活性参数构建QSPR/QSAR模型，并对其性质进行评估与预测，已成为化学研究中异常活跃的领域之一，近年来越来越受到化学工作者的重视并且发展迅速。1

构造拓扑指数有3个基本的要求：

(1)拓扑指数应为一个或一组数据，即分子图拓扑不变量的数值化；

(2)能充分反映分子图的连接信息和化学环境；

(3)能有效地表达化合物结构与性质(活性)的关系。

拓扑指数能用于描述化学结构，并且与化合物的物理性质、热力学参数、化学性能，生物活性以及致癌性相关。2

应用比较广泛的有4 种拓扑指数：分子连接性指数、电拓扑状态指数、分子电性矩矢量及Kappa 指数。1

分子连接性指数分子连接性指数(MIC)是基于分子二维拓扑结构最重要的指数之一，可用于处理含环、多重键和含杂原子的分子体系，它与分子极化度、水溶性、沸点等多种物理化学性质存在良好的相关性。多年来，分子连接性指数在各领域的应用中取得了丰硕的成果，但由于MIC 法主要局限于描述化合物的立体结构，而反映化合物的电子结构的能力较弱，实践中也暴露了一些弱点。因此，很多学者致力于新型MIC 指数的开发，以求更为全面、细致的描述分子的结构特征，进一步扩展分子连接性指数的应用范围，部分新型MIC 指数如图所示。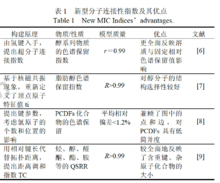

分子连接性指数有诸多优点，其建立的参数不受实验值或经验值限制；计算简单、容易掌握；灵活性较强且能借鉴量子力学的某些指数。不足之处在于它主要局限于描述化合物的立体结构，不能充分反映化合物的电子结构，但通过研究者们大量的探索和改进，已经提出了许多更全面、物理意义更加明确的分子连接性指数。1

电拓扑状态指数化合物中起主要作用的可能仅仅是分子中的某个原子或分子片断，分子水平指数很可能无法确定化合物分子中决定活性的特征原子。因此，Kier 与Hall 等人提出了一种新型电拓扑指数，它是根据分子隐氢图中每个非氢原子所处的拓扑环境及成键电子状况而建立的，能够表明原子电子特性和分子中每个骨架原子的拓扑环境。此类拓扑指数计算快速、操作容易且易于解释，已发展为电拓扑状态指数(electrotopological stateindices, En) 和原子类型电拓扑状态指数(Electrotopological State Indices for atom type, ETSI)两种，广泛用于构建在原子水平和不同原子类型形式下的QSAR 相关模型。

电拓扑状态指数能够充分表征化合物分子本身的立体结构、取代基、电性效应影响等性质。它更好的描述了分子中原子或基团之间的相互作用及其影响，可被快速计算，有着高度的可应用性。可用于建立有机化合物理化性质、毒理学性质与分子结构之间的相关关系模型，在QSAR 建模中已得到成功、广泛的运用，并且具有广阔的应用前景。1

分子电性距离矢量分子电性距离矢量(Molecular ElectronegativityDistance Vector，MEDV)是一种描述分子二维结构的拓扑描述子，最初由刘树深等人提出。MEDV 引入了相对电负性和相对键长的概念，适用于含多个杂原子、饱和键与不饱和键、环和非环等结构特征，具有良好分辨率和高度相关性，是一种通用性更强的新型描述子。分子电性距离矢量己用于各种定量结构与物理化学性质和生物活性的研究中。

分子电性距离矢量计算简单，结构参数的取值完全来自分子本身的结构，不需要加入任何经验性的性质参数或校正参数，较为客观，且计算易程序化，只需要输入分子中原子及其连接关系就能很容易得到。它不只是应用于具有相似结构的同类化合物的QSRR 研究，还能较好地表征非同类化合物的分子结构信息，在有机物QSRR 研究上有较强的普适性。但作为一个二维拓扑描述子，MEDV 在描述旋光异构、顺反异构的化合物结构和分子的实际结构时，尚有一定的局限性。1

Kappa(分子形状)指数用于表征分子形状的拓扑指数有Kier 的Kappa 形状指数(mK)及Randic 的分子形状描述符。下面主要介绍由Kier 和Hall 提出的Kappa 指数，它反映的是分子形状和分子的柔性。

Kappa指数中的1 K所显示的结构信息主要为分子结构的复杂度，确切地说反映了分子的环性程度；2K主要揭示分子中原子的空间密度，均有一定的优点。但是，由于mK对分子的结构选择性较低，不能区分邻、间、对位取代的异构体，因此mK指数在建模时一般都与其它类型的拓扑指数结合使用，如上述电性拓扑状态指数、取代基定位参数、取代基距离参数等，联合使用可以取长补短，使所构建的模型相关性良好。1

分子结构的数值化有机分子的拓扑指数应用研究是现代计算化学, 结构化学与量子化学相互交叉和结合的产物, 已成为当前信息化学的重要分支。

实验表明, 分子的许多性质首先受制于分子的拓扑结构一原子的连接性田。这些性质包括分子的宏观热力学性质, 如沸点、分子体积、折光率等, 也包括分子的微观特性。除此之外,生物活性也可以从分子拓扑加以解释图。这就启发化学家从一个侧面去总结结构与性质的定量相关关系。应用拓扑指数提炼分子信息要经过分子结构的图形化, 矩阵化和数值化三个步骤。

化学结构本身是抽象的, 难以定量抽述, 而它们的各种物理化学性质则表现为一定的数值。抽象的结构与用数值表达的性质间无法进行定量的关联。因此, 对结构的数值表征的研究十分必要。通过对分子图的矩阵实施某种数字运算而获得的拓扑指数, 建立了结构和一个无量纲数据间的一一对应, 实现了结构的数字形式的表达。

自1947年第一个能表征分子的“ 支链性”的拓扑Wiener指数指数田提出后, 又出现了多个拓扑指数, 但只有很小一部分与分子的性质有较好的相关性能。常用的几种拓扑指数都是建立在距离矩阵或邻接矩阵及其不变量的基础上。3

发展趋势自1947 年第一个拓扑指数-Wiener 指数W 问世以来，化学工作者一直在寻找一种能惟一表征不同化合物的图的不变量，即发展高选择性的拓扑指数。一般来说，对新构建的拓扑指数有2 个基本的要求：一是与化合物性质有良好的相关性；二是具有良好的惟一性。研究者们在提出新型拓扑指数时，主要有4 个方面的发展趋势：

(1) 通过重新定义原子点价，对原拓扑指数进行修正；

(2) 将拓扑学与量子化学等方法结合起来，构建新的量子拓扑参数；

(3) 在构建模型时，把不同的拓扑参数联合使用，取长补短，使所构建的模型具有更好的相关性；

(4) 原子点价(δi)向着能反映成键原子价层空间的三维立体结构拓展。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学