[科普中国]-章动常数

章动常数是天文常数之一。真天极绕平天极在18.6年内描绘出一个小椭圆，称为章动椭圆（见岁差和章动）。章动椭圆的中心在平天极，椭圆的长轴指向黄极方向，短轴指向春分点方向。

概述章动椭圆的半长径称为章动常数，用N表示。章动常数可根据恒星位置或纬度的观测资料来确定。

历史十九世纪末，纽康总结了以前的观测资料，由27个测定值求加权平均得。

该值在1896年巴黎的国际基本恒星会议上被采纳，一直沿用。1976年在国际天文学联合会第十六届大会上，通过了对于标准历元2000年的新值N=9.2109"。

编制天文年历所依据的章动理论是伍拉德在1953年建立的，它是以刚体地球模型为基础的。二十世纪以来，根据观测资料得出的章动常数，都与采用值有一定差异，因为地球并不是一个刚体。1977年国际天文学联合会关于章动和地球自转的第78次讨论会，决定为修改章动常数成立一个专家工作组。这个工作组建议采用非刚体地球模型──莫洛坚斯基第Ⅱ模型代替刚体地球模型来计算章动。新建议的章动常数不再采用观测值，而是依据月地质量比、日月岁差和章动常数之间在理论上已知的关系，先求出刚体地球的章动常数，然后换算成非刚体地球的数值。对于标准历元2000年，N=9.2044"。1979年国际天文学联合会第十七届大会正式通过了这一建议，并决定于1984年正式采用。

主章动常数和对它的天文实测作为一 个基本的天文常数，主章动常数的实测有其重要的意义。早在十九世纪末，对它的天文实测结果就有近30个之多。在此基础上纽康取其权平均，得到N=9.2109"。这个主章动常数值一直被沿用到1983年。它已被国际天文学联合会通过的1980IAU章动理论中的N=9.2025"所取代。但是，一些研究指出，这个新的主章动常数很可能仍存在着几个毫角秒的误差。如果真是这样，对测量精度已达到了毫角秒级的天体测量新技术来说，这是一个值得注意的问题。1

在纽康时代，主章动常数是一个由实际测量值定义的天文常数。但它已成为由理论研究得到的章动理论(或称章动序列)中的一组常数，当然也是最大和最重要的一个组成部份。由于人们已经精确地测定了日、月、地球的质量、它们之间的相对位置和运动，精确地计算出日、月在地球上产生的引潮力，因此，章动作为地球对这种引力的一种响应，也就由此而得到。当然，这还有赖于对地球本身情况的了解。不同的地球模型，计算出来的章动也不一样。

于是，我们就要提出这样一个问题：由一种技术的观测得出的一个地球模型，是否能符合另一种技术的观测呢？这当然是不一定的。因为，不同的技术有其不同的特性和局限，所谓一个地球模型，从根本上来说只不过是对某种技术的某个观测子样的一个拟合，它不一定也同时适合于另一种技术、另一个观测子样的要求。所以，从不同的技术、不同的观测子样去研究地球模型，其结果往往是不一样的。

如果上面的这个观点是正确的，下面的几点将是可能的：

基于地震观测得到的1066-A地球模型，尽管地球物理界在一段时间内曾认为它是最优的，并不一定也同样地适合于天文观测；

基于1066-A地球模型的1980IAU章动理论，可能与天文观测存在一定的偏差；

从原则上讲，天文观测技术可以对各种章动理论以至于相应的地球模型作出独立的判断，进而选择一种最优的章动理论。

全面地讨论这些问题已超出本文的范围。研究的主要目的是列举天文观测的事实，进而说明就主章动常数而言，IAU在1982年通过的1980IAU章动理论已未必是一种足够精确的理论了。对它作进一步研究和改进，是有其必要的。

实际测量主章动常数的天文方法（1）基本公式

章动，即真级相对于平级的运动，可以用交角章动 和黄经章动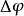 来表示。由于天文观测资料往往按约定的章动理论归算，所以在测量中实际解算的则是它们的改正数 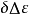和 ；在对章动项进行实测时，无非是将上述改正数与实际观测值相联系，组成观测方程式。当观测方程式的数目多于欲求的未知数时，就可以按最小二乘法进行求解。

例如在时间纬度测量时，可按下述两个关系式组成观测方程式：

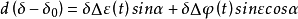
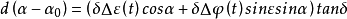其中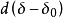 、 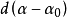是在天体上（α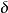， ）处，因采用的章动理论不完善所导致的赤纬、赤经误差。当它们是已知值时，就可以对章动项振幅的误差进行求解。

（2）影响主章动常数测量精度的几个主要因素

为 了能更好地提高主章动常数的测量精度，有必要进一步在理论上讨论影响主章动常数实测精度的稳定性。测量真极在天球上的运动时，其结果直接受到所测天体在天球参考系中坐标误差的影响。但是就主章动常数的测量而言，不同性质的坐标误差其影响也不是一样的。如果在整个过程中始终观测同一组恒星或同一颗射电源，那么天体的星位误差和自行误差中的线性成份，并不会影响主章动项的测量结果。因为它们完全被观测方程式中的常数项和线性项所吸收了。但是就章动的实际测量而言，往往要观测多组恒星或多个射电源。正确地对观测天体的星位误差和自行误差进行改正就成为一件重要的事。而这正是过去用光学技术对章动进行天文实测时还没有解决好的一个关键问题。另一方面，当所测天体的坐标中还存在着其他性质的误差成份时，情况就不完全一样。特别是当所测天体的坐标中存在着与所测章动项相同周期的误差成份时，该项系统性质的误差将因无法被分离而进入到章动的测量值中去。在用激光测距技术(LLR)进行主章动常数的测量时就会碰到这种情况。月历表的不够准确会明显影响测量结果的精度，使所得的主章动常数难于突破4-11毫角秒的精度水平。在这一点上，甚长基线射电干涉测量(VLBL)技术的情况就要好得多。因为它观测的射电源是一个稳定的测量目标。

主章动常数的光学天文测定在本世纪七十年代以前，光学天文技术是直接测量主章动常数的天文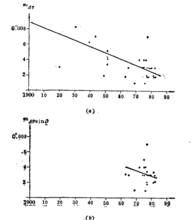手段。从图1所示的测量误差可以看出。在本纪七十年代光学技术达到鼎盛时期以前，主章动常数两个分量的测量精度一直在提高；但中误差 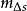、 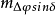分别达到±0.002"和±0.003"的水平以后就有些停滞不前了。而当时，正值IAU在讨论决定新章动理论的关键时刻。这样的精度水平就使得当时的天文实测工作没有能够在检验几种可供考虑的章动理论中起到应有的作用。

正是在这样一种形势下，ILS和IPMS的Yumi，BIH的Giunot、Feissel都开始对过去天文观测资料的全面整理和修正工作。这样一份极其丰富的历史天文资料，能否对主章动常数的实测作出一些新的贡献呢?

本文作者之一1982-1984年在BIH曾全面修正了全球136架天文时纬仪器在1962.0-1982.0年间的50万个测量数据，使之均质化。还改变了过去以一架仪器作为时间或纬度观测序列的集合单位的传统做法，以观测星组作为基本的集合单位。并对这样的观测序打定义两个星组未知数G和G"，用以改正该星组固有的星位误差和自行误差。对全球数千个以星组为集合单位的测量序 列采用整体解算的方法，在归算20年的地球自转参数(ERP)的同时，也对数千个固定星组的G、G"进行解算。这一系列做法不仅显著地提高了ERP的精度，也大大提高了同时得到的两个辅助参数z、w的精度。2

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学