[科普中国]-球面三角

球面三角是研究球面三角形的边、角关系的一门学科。从十六世纪起由于天文学、航海学、测量学等方面的发展，球面三角逐渐形成了独立学科。从平面三角学我们知道，一圆周的1/360 ，叫做1度的弧。1度弧的1/60 叫做1角分的弧。1角分弧的1/60 叫做1角秒的弧。根据弧和所对圆心角的关系，可以得出角的量度。一圆周所对的圆心角为360°。因此，1度的弧所对的圆心角，叫做1°的角；1角分的弧相对的圆心角，叫做1′；1角秒的弧所对的圆心角，叫做1"。

球面三角初步基础知识天文学，特别是球面天文学需要球面三角学的知识。球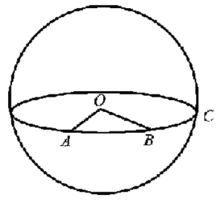面三角中，常要用到角度和圆弧的度量关系。从平面三角学我们知道，一圆周的1/360，叫做1度的弧。

角和弧的量度单位，常用的有两种：

弧度：长度和半径相等的圆弧所对的圆心角，叫做1弧度（rad）。

由于一圆周的长度等于2π个圆半径的弧长，根据以上弧度的定义，得到弧度和度的关系如下：

2πrad=360°；

1rad= 360/2π =57.3°= 3438′= 206265"；

或者 1°=1/57.3 rad；

1′=（1/60）°=1/3438 rad；

1"=（1/60）′=1/206265 rad。

如果一个角的值以弧度表示时为θ，那么以度表示时其值为57.3°×θ；以角分表示时为3438′×θ；以角秒表示时为206265"×θ。为了方便起见，我们用符号θ°，θ′，θ"表示一个角的度数、角分数、角秒数。

θ°=57.3°θ，θ′=3438′θ，θ"=206265θ"。

当角度很小时，角度的正弦或正切常可以近似地用它所对的弧来表示。

例如：sin1"≈tan1"≈1"=1/206265 rad

由此得：1rad=206265"=206265 sin1"

根据相同的理由，得：sinθ"≈tanθ"≈θ"= θ/206265=θsin1"

上式常写为：θ=θ"sin1"

球面上的圆：从立体几何学得知，通过球心的平面截球面所得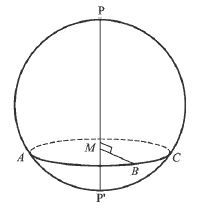的截口是一个圆，叫做大圆；不通过球心的平面截球面所得的截口也是一个圆，叫做小圆。通过球面上不在同一直径两端的两个点，能做并且只能做一个大圆。

例如通过图1中的任意两点A和B，也仅可以做一个大圆ABC。A、B两点间的大圆弧（小于180°的那段弧）可以用线长、也可以用角度计量，在天文上常用角度来计量，叫做A、B间的角距，记为⌒AB（⌒应该画在AB的上方，下同） ，它等于大圆弧⌒AB所对的中心角∠AOB。

球面上圆的极：设⌒ABC为球面上的一个任意圆（图2），它所在的平面为MABC，又设PP’为垂直于平面MABC的球直径，则它的两个端点P和P’叫做圆⌒ABC的极。如果用一句话来表达，可以这样说：垂直于球面上一已知圆（不论大圆或小圆）所在平面的球直径的端点，叫做这个圆的极。

球面上某一圆的极和这个圆上任一点的角距，叫做极距。可以证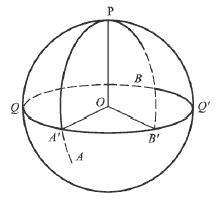明，极到圆上各点的角距都是相等的；如果所讨论的圆是一个大圆的话，则极距为90°。

球面角：两个大圆弧相交所成的角，叫做球面角。它们的交点叫做球面角的顶点。大圆弧本身叫做球面角的边。图3绘出了两个相交的大圆弧⌒PA和⌒PB，O为球心，⌒PA所在的平面为POA，⌒PB所在的平面为POB，两者的交线为OP。球面角∠APB用POA和POB所构成的两面角来量度。在图3中做以P为极的大圆⌒QQ’，设⌒PA（或其延线）和⌒QQ’相交于A’，⌒PB（或其延线）和⌒QQ’相交于B’，则由于P为⌒QQ’的极，所以OP垂直于平面QQ’，因而也垂直于OA’和OB’，所以∠A’OB’就是平面POA和POB所构成的两面角。即：球面角∠APB可以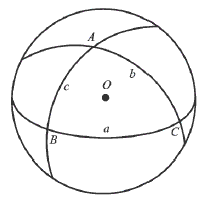用∠A'OB'量度，又因为∠A'OB'可以用 A'B'量度，所以最后得到的球面角∠APB是以⌒A'B'弧量度的。

从上面的讨论可以概括出下述结果：如果以球面角的顶点为极作大圆，则球面角的边或其延长线在这个大圆上所截取的那个弧段便是球面角的数值。

球面三角形：把球面上的三个点用三个大圆弧联结起来，所围成的图形叫做球面三角形。这三个大圆弧叫做球面三角形的边，通常用小写拉丁字母a、b、c表示；这三个大圆弧所构成的角叫做球面三角形的角，通常用大写拉丁字母A、B、C表示，并且规定：A角和a边相对，B角和b边相对，C角和c边相对（如图4所示）。三个边和三个角合称球面三角形的六个元素。1

基本公式极三角形：设球面三角形ABC各边a、b、c的极分别为A'、B'、C'（图5），并设弧⌒AA'、⌒BB'、⌒CC'都小于90°，则由通过A'、B'、C'的大圆弧构成的球面三角形A'B'C'叫做原球面三角形的极三角形。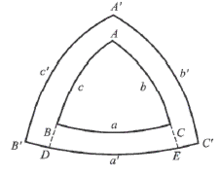

极三角形和原三角形有着非常密切的关系，这种关系存在着两条定理。

定理1：如果一球面三角形为另一球面三角形的极三角形，则另一球面三角形也为这一球面三角形的极三角形。这条定理很容易证明，请读者自证。

定理2：极三角形的边和原三角形的对应角互补；极三角形的角和原三角形的对应边互补。

证明：B'是b的极（图F3.5），C'是c的极，所以有：

⌒B'E=⌒C'D=90°；⌒B'E+⌒C'D=180°。

即⌒B'C'+⌒DE=180°

但由定理1，A是⌒B'C'的极，故有⌒DE=A，将此式以及⌒B'C'=a'代人上式，便得到

a'+A=180° （1.1）

（1.1）式即定理2的前半的证明。定理2的后半不需证明；因为实际上，它只是定理1和定理2的前半的一个推论。

边基本性质1．球面三角形两边之和大于第三边。

证明：将球面三角形ABC的顶点和球心O连结起来（图6），由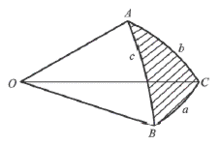立体几何得知：三面角的两个面角之和大于第三个面角，即∠AOB+∠BOC>；∠AOC。故c+a>b。同理a+b>c，a+c>a。

推理：球面三角形两边之差小于第三边。

2．球面三角形三边之和大于0°而小于360°。

证明：因为a，b，c均为正，故a+b+c>0°，又由立体几何得知凸多面角各面角之和小于360°，因此∠AOB+∠BOC+∠COA