[科普中国]-生物电阻抗断层成像重构算法

电阻抗断层成像(Electrical Impedance Tomography，EIT)重构算法的目的是通过电流激励区域边界上的电压值重构出区域内部的电阻抗分布。重构算法一般分为两种，一种是重构出电阻抗绝对值的静态算法，一种是重构出电阻抗相对变化值的动态算法。由于测量数、边界形状等一系列实际条件的限制，重构图像只能给出一个真实电阻抗的估计。

1.正问题生物体的电磁场规律都可以用麦克斯韦（Maxwell）方程组表示：

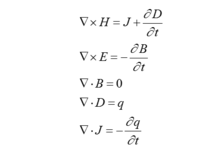
其中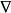， 为矢量微分算子(泊松算子)，E为电场强度，D为电感应强度，B为磁感应强度，H为磁场强度，J为传导电流密度。电、磁场中的场量E、B与D、H之间的关系由媒质的特性决定，在各向同性的媒质中，它们有如下关系：

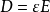
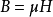
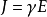
其中，ε为复介电常数；μ为导磁率；γ为电导率。在我们所观察的电流场中，没有孤立电荷存在，因而电荷密度为0，在较低频率下，可以忽略介电常数的影响，又因成像目标内部无自由电荷，从而得到以下方程(拉普拉斯方程)：

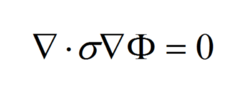
其中，σ为纯电导率，对应的边界条件为：

在进行EIT正问题分析时，可以将区域Ω分为许多离散的单元，每个小单元内有一个均匀电阻抗的分布，可以得到离散域的一个线性化的等式，以矩阵的形式写为：

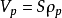
其中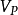，是测量电压变化值矢量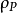，是离散电阻抗变化矢量，S是敏感系数矩阵，其中的系数可以表示为：

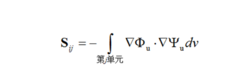
其中i代表第i个驱动测量对，j代表第j个单元，积分则是对单元容积的积分。

2.逆问题建立EIT正问题后，可以将EIT图像描述看成一个逆问题的求解，即已知激励电流和边界电压求解内部电阻抗变化。我们就可以通过对敏感矩阵进行求逆来获得电阻抗变化的分布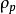，因此有：

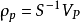
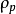给定边界测量值，我们可以计算扰动的电阻抗图像。这个结果对任何维数和电极安排都是有效的，但是电极的位置和电极对的驱动测量方式都会影响到敏感矩阵的形式以及矩阵逆的稳定性，进一步影响图像的重构质量。

3.逆问题正则化针对线性离散正问题，我们假设不含噪声的理想状态下：

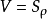
其中V为测量值向量，大小为M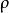，为未知的模型参数向量，大小为N，S为敏感矩阵，大小为（M×N）。在EIT的研究中，ν指边界电压测量值的变化量，为内部电阻抗的变化量，S其为敏感矩阵，其逆问题可表示为：

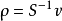
其中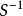为S的逆，在大多数情况下，测量值通常只能在连续域的几个独立点上进行测量获得，而模型参数理论上讲在域内有无穷多个，因此可以认为M