[科普中国]-动态电阻抗断层成像反投影重构算法

反投影法是EIT领域最为经典的一种动态算法，该算法首先由Barber 等人在1983年提出，并由他在1990年用新的形式进行了表示。许多研究小组实现了反投影法，其中很多都采用的是临近的激励和测量方式。

Barber的反投影算法借鉴了传统X线断层成像的技术。Barber等人取代传统X线直线反投影的方式，而将归一化后的边界测量值沿着等式线来反投影，而这些等势线是通过激励电流的位置和大小来计算出来的，它从一个测量电极队延伸到另外一侧的边界并与电流方向垂直。

1.反投影重建过程反投影重建时，首先通过电磁场计算，在均匀背景下获得激励电流产生的等势线，图1所示是将两个离散并分开的电极等效为电流源的偶极子模型下的等势线。

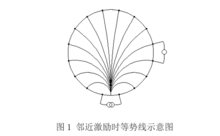
图1 邻近激励时等势线示意图

对于临近驱动，共有16个驱动，每一个电极驱动都可以测量到13个有效电压值。如果电阻抗变化非常小，则可以假设与均匀背景相比，等势线的形状不会发生改变，但是他们的测量值会由于电阻抗的扰动而发生改变，反投影法正是将这些电压变化值进行反投影，如图2所示，所有两个测量电极对应的两条等势线之间的区域内所有像素都赋予相应的电压变化值 。

图2 反投影法重构过程

经过重构和处理后，即可得到如图3所示的图像。

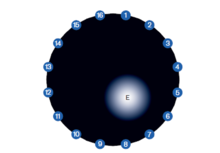
图3 反投影法重构结果

2.局限性反投影重构算法实现较为简易，加之良好的抗噪性能，在EIT研究早期具有重要的作用。但是由于该算法是直接借鉴CT成像算法，所以理论推导并不严谨，所重构的图像空间分辨率很低，模糊效应和拖尾伪影较为严重，近年来已逐渐被最小二乘等最优化算法所取代。

3.扩展阅读[1] BH Brown and DC Barber. ‘Applied Potential Tomography’ – a new in-vivo medical imaging technique. Proc. of the HPA Ann. Conf., Sheffield, 1982.

[2] JP Morucci and PM Marsili. Bioelectrical impedance techniques in medicine. Part Ⅲ: Impedance imaging. Second section: reconstruction algorithms. Crit Rev Biomed Eng 1996, 24(4-6): 599-654.

[3] AV Korjenevsky. Reconstruction of absolute conductivity distribution in electrical impedance tomography. Proc. IX Int. Conf. Electrical Bio-Impedance(Heidelberg), 1995, 532-535.

[4] N. J. Avis and D. C. Barber. Incorporating a-Priori Information into the Sheffield Filtered Backprojection Algorithm. Physiol. Meas., 1995, 16: A111-A122.

[5] B. H. Brown and A. D. Seagar. The Sheffield data collection system. Clin Phys Physiol Meas, 1987, 8 Suppl A: 91-97.

本词条内容贡献者为:

徐灿华 - 讲师 - 第四军医大学生物医学工程学院董秀珍 - 教授 - 第四军医大学生物医学工程系