椭圆型偏微分方程,简称椭圆型方程,一类重要的偏微分方程。早在1900年D.希尔伯特提的著名的23个问题中,就有三个问题是关于椭圆型方程与变分法的。八十多年来,椭圆型方程的研究获得了丰硕的成果。椭圆型方程在流体力学、弹性力学、电磁学、几何学和变分法中都有应用。拉普拉斯方程是椭圆型方程最典型的特例。
定义椭圆型偏微分方程是偏微分方程的一个类型,简称椭圆型方程。这类方程主要用来描述物理只能的平衡稳定状态,如定常状态下的电磁场、引力场和反应扩散现象等。
椭圆型方程是由方程中主部的系数来界定的。对两个自变量的二阶线性或半线性方程
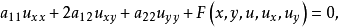 在不等式
在不等式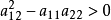 成立的区域内,就称方程是椭圆型的。
成立的区域内,就称方程是椭圆型的。
此时,可以通过自变量的非奇异变换将方程化为标准型
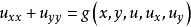 对于高阶线性方程,设
对于高阶线性方程,设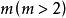 阶线性偏微分算子为
阶线性偏微分算子为
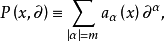 其中,
其中,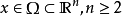 。该偏微分算子的主部是
。该偏微分算子的主部是
 若对
若对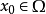 及任意非零向量
及任意非零向量 都有
都有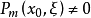 ,则称方程
,则称方程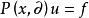 在点
在点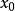 是椭圆型的。如果
是椭圆型的。如果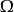 中是线性椭圆型方程。
中是线性椭圆型方程。
种类线性线性椭圆型方程的典型代表是拉普拉斯方程(也叫调和方程)
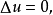 其中,
其中,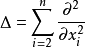 ,这个算子叫拉普拉斯算子 (Laplace operator),也叫调和算子。
,这个算子叫拉普拉斯算子 (Laplace operator),也叫调和算子。
可以说,调和方程是最基本,同时也是最重要的线性椭圆型方程。
非线性对于非线性方程,也可以定义椭圆型方程。
例如,考虑二阶实系数拟线性方程
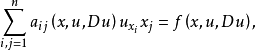 其中,
其中,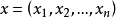 。如果对任意非零向量
。如果对任意非零向量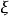 ,
,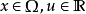 及
及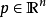 ,有
,有
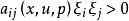 就称方程是
就称方程是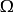 中的拟线性椭圆型方程。类似地,可以定义高阶拟线性椭圆型方程。1
中的拟线性椭圆型方程。类似地,可以定义高阶拟线性椭圆型方程。1
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国