数学真正意义上研究退化和奇异抛物偏微分方程是近些年才开始的,起源于60年代中叶DeGiorgi,Moser,Ladyzenskajia和Ural’tzeva这些人的工作。退化抛物方程是近些年来该领域的进展的综述,其基本思想来自上个世纪90年代作者在波恩大学的Lipschitz讲义。
定义数学真正意义上研究退化和奇异抛物偏微分方程是近些年才开始的,起源于60年代中叶DeGiorgi,Moser,Ladyzenskajia和Ural’tzeva这些人的工作。
退化抛物方程是在某些点退化的抛物型方程。
一个线性抛物型方程可写成如下形式:
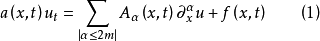 其中,算子
其中,算子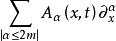 的主部
的主部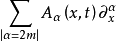 满足椭圆型条件。
满足椭圆型条件。
如果在所讨论的区域中的某些点上 a(x,t)=0 或者算子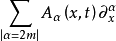 退化(见退化椭圆方程),就称该方程为退化抛物方程。
退化(见退化椭圆方程),就称该方程为退化抛物方程。
举例非线性退化抛物型方程的一个典型例子是多孔介质方程
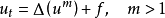 它在 u=0 处退化。
它在 u=0 处退化。
辨析退化抛物型方程与非退化抛物型方程的性质有许多重要的差别。
例如,非退化的抛物型方程具有扰动无限传播性质 (infinite propagation property),而退化抛物型方程可能具有扰动的有限传播性质 (finite propagation property)。1
相关概念函数空间数学中,函数空间指的是从集合X 到集合 Y 的给定种类的函数的集合。其叫做空间的原因是在很多应用中,它是拓扑空间或向量空间或这二者。经典分析学研究中出现了许多重要的函数空间。对一些类型的函数空间,现已取得相当丰富的理论成就。
弱解数学中,微分方程的弱解或广义解是指对该方程中的微分可能不存在,但是在某种精确定义的意义下满足该方程的解。对于不同种类的微分方程,弱解的定义性质也可能不同。 一类最重要的弱解基于广义函数的记号。
退化在数学中,退化是指在一个在一个限制的情况下,一个集合中的对象改变其性质并且属于另一个集合,通常是变成比较简单的集合,例如,一个三角形是一个平面集合的一个对象,但是若改变其性质将单一内角改为180度使其边皆重合,则它就属于线段集合的一个对象,且线段这个集合比平面还要简单,因为它少一个维度,我们就会称此多边形退化了。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国