[科普中国]-二阶平稳假设

当区域化变量满足下列两个条件时，则称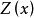满足二阶平稳(或弱半稳)1：

①在整个研究区域内，区域化变量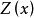的数学期望存在且不随位置发生变化，即

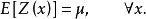
②在整个研究区域内，区域化变量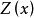的协方差函数存在，且仅依赖于滞后距离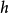，与无关，即

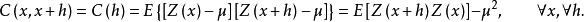
二阶平稳假设假定研究区域化随机变量的协方差存在，实际就是假设了区域化变量有一个有限的先验方差。当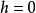时，有

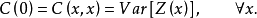对相关函数可写成

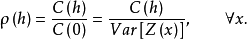
简单而言，二阶平稳假设是讨论区域化变量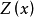本身的特征，而本征假设是研究区域化变量增量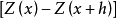的特征。一般而言，二阶平稳假设对区城化变量要求较严，本征假设要求较弱。也就是说，如果某个研究区域区域化变量是二阶平稳的，那么它一定是本征的；反之，若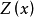是本征的，则不一定是二阶平稳。

由二阶平稳假设的第一个条件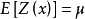，显然可以推导出本征假设的第一个条件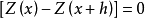，。但由本征假设的第一个条件，只能推导出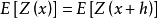，无法肯定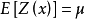是否成立。在一般情况下，对任意一组数据都可求出它们的均值，但这个均值并不一定等于这个研究区域的数学期望值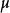。因此，本征假设容许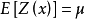不成立，所以区域化变量满足本征假设不一定满足二阶平稳假设。

由二阶平稳的两个条件可以推导出本征假设的第二个条件:

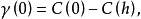由上式可见，只要区域化变量的协方差存在，则半方差函数一定存在。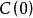为区域化变量的方差，即二阶平稳假设事先暗示了区域化变量的方差存在，因此这个方差又称为先验方差1。

如果区域化变量只在有限区城内是二阶平稳的或是本征的，则称此区域化变量是准二阶平稳的或准本征的。准二阶平稳或准本征假设是一种折中方案，既要考虑到平稳或本征的范围大小，又要顾及有效数据的多少。如果范围确定大了，往往不易满足二阶平稳或本征假设的条件；若范围确定太小，则区域内的数据就太少。放确定范围的大小应兼顾上述两方面1。