[科普中国]-频率失真

运算放大器广泛应用在各种电路中，不仅可以实现加法和乘法等线性运算电路功能，而且还能构成限幅电路和函数发生电路等非线性电路，不同的连接方式就能实现不同的电路功能。集成运放将运算放大器和一些外围电路集成在一块硅片上，组合成了具有特定功能的电子电路。集成运放体积小，使用方便灵活，适合应用在移动通信和数码产品等便携设备中。

但在实际工程应用中，由于种种原因，总是会出现输入波形不能正常放大，这就是放大电路的失真现象。失真现象主要有两大种类型：线性失真和非线性失真。造成线性失真的主要原因是放大器的频率特性不够好。而造成非线性失真的原因有晶体管等特性的非线性和静态工作点位置设置的不合适或输入信号过大。1

非线性失真亦称波形失真、非线性畸变，表现为系统输出信号与输入信号不成线性关系，它与线性失真的本质差别是由电子元器件的非线性所引起，使输出信号中产生新的谐波成分，改变了原信号频谱。造成非线性失真的原因主要有晶体管等特性的非线性和静态工作点位置设置的不合适或输入信号过大。由于放大器件工作在非线性区而产生的非线性失真有一下几种：饱和失真、截止失真、双向失真、交越失真、谐波失真、互调失真、不对称失真、瞬态互调失真。2

在放大电路的输入信号是多频信号时，如果放大电路对信号的不同频率分量具有不同的增益幅值，就会导致输出波形发生失真，称为幅度失真；如果相对相移发生变化，称为相位失真，这两者统称为频率失真。频率失真是由电路的线性电抗元件引起的，频率失真的特征是输出信号中不产生输入信号中所没有的新的频率分量。如右图，为输入多频复杂信号时经过放大电路后产生相位失真和幅度失真的信号波形。造成线性失真的原因主要是放大器的频率特性不够好。

根据上述原因，频率失真可分为幅度失真和相位失真。

由傅立叶分析的基本理论，任何一周期信号都可以分解为直流分量，基波分量和各次谐波分量的加权。而谐波就是频率为基波整数倍的余弦信号。若为基波的N倍，即称为N次谐波。可见，如果一个系统对不同频率分量的放大倍数不同，那么对不同的谐波分量将有不同的放大倍数。当一个信号通过系统之后，各谐波分量的幅度发生了改变，加权后将不能真实反应原信号。

从相位的角度来考虑，如果原信号的各次谐波通过这个系统，产生了不同的相移（表现为时域为不同的延迟），则系统输出的各次谐波加权之后，也不能真实反应原信号。

在我们日常生活中，语言、图像、音乐等信号都是由基波分量和谐波分量叠加而成的复杂信号，如对于一部电话机、频率失真很小时，从电话中双方还能相互分清；失真严重时甚至无法辨清对方性别，又如对电视图像信号来说，若视频放大器产生高频失真将使图像细节不清晰；低频失真时则造成背景亮度不均匀。对器乐合奏来说，当扩音器产生高频失真将使乐音失去原有特色，给人以单调乏味的感觉，甚至无法听；低频失真则使浑厚雄壮的乐曲变得轻浮无力，这是因为基波分量决定音调和谐波分量决定音色的缘故为了减小频率失真，使输入信号中的高低频分量均获得与中频同样的增益，必须展宽放大器的通频带，使信号中的高低频分量都处在通频带范围内。

放大器的实际输入信号通常是由许多频率分量按照一定的幅度比例关系和相位关系叠加而成的非正弦信号。在放大器中由于器件的电抗效应和电抗性元件的存在，使得放大器对不同频率信号具有不同的放大能力，即放大器的增益随频率不同而改变。影响低频增益的主要因素是耦合电容和旁路电容，影响高频增益的主要是结电容和引线等的杂散电容。为了减小这些因素带来的频率失真，使输入信号中的高低频分量均获得与中频同样的增益，必须展宽放大器的通频带，使其在工作频率内（如音频为20HZ-20KHZ）近似满足无失真传输条件。

常用的展宽通频带的方法有三种：补偿电路法、负反馈法、组合电路法。

（1）补偿电路法：补偿电路法如右图中图1。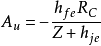，。输入高频时，减小，增大，频带得到适当展宽。

（2）负反馈法：在加入负反馈后，如右图中图2所示。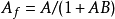，，。可以看出，加入负反馈后，增益下降，但是频带却得到了展宽。

（3）组合电路法：通过不同组态电路组合，改变电路的时间常数，提高高频截频。常用的有低阻输入的共射-共基电路和低阻输出的共集-共射电路，这几种组合电路均可以提高截频。

但是在实际工程研究和应用中，受晶体管特性等影响，通频带是不能无限展宽的，而且在展宽通频带的同时，会带来其它弊端，尤其是会引入噪声。所以不同的放大器，可以选择不同的展宽频带方法，频带宽度可以视要求而定。3