三角形单元适应性强,能适应各种曲折的几何边界,但是它的位移函数阶次较低,为常应变单元、精度较低,不能反映实际应力的变化情况。而矩形单元的精度高,但适应性差,遇到曲线边界或非直角的直线边界难以模拟。虽然可以混合使用两种单元,但增加了数据准备的工作量。而采用等参数单元,能在同等精度下,可以用较少的单元去求解实际结构。一方面,单元能很好地适应曲线边界和曲面边界,准确地模拟结构形状;另一方面,这种单元要具有较高次的位移模式,能更好地反映结构的复杂应力分布情况,即使单元网格划分比较稀疏,也可得到较好的计算精度。等参数单元(等参元)就具备了以上两条优点,因此,得到广泛应用。
等参数单元(简称等参元)就是对单元几何形状和单元内的参变量函数采用相同数目的节点参数和相同的形函数进行变换而设计出的一种新型单元。由于等参变换的采用使等参单元的刚度、质量、阻尼、荷载等特性矩阵的计算仍在前面所表示单元的规则域内进行,因此不管各个积分形式的矩阵表示的被积函数如何复杂,仍然可以方便地采用标准化的数值积分方法计算。也正因为如此,等参元已成为有限元法中应用最为广泛的单元形式。同时,等参单元具有计算精度高和适用性好的特点,是有限元程序中主要采用的单元形式。2
基本思想先将在局部坐标系中简单几何形状的单元,称为母单元。按照高阶插值多项式来构造形状函数,形成局部坐标系的单元位移函数然后通过坐标变换,将简单几何形状的母单元在总体坐标系中映射成实际网格划分的曲边或曲面单元。
实际单元的特性分析(位移、应变、应力等)就可借助基本单元(母单元)来进行,再将分析结果变换(映射)到实际单元去。由于基本单元形状规则,因此位移模式容易选取,计算也大为简单。
等参数单元在构造形函数时首先定义一个规则的母体单元(参考单元/ 标准单元),在母体单元上构造形函数,再通过等参数变换将实际单元与母体单元联系起来。
变换涉及两个方面:几何图形的变换(坐标变换) 和位移场函数的变换(母单元的位移模式)分别如图1、图2所示。
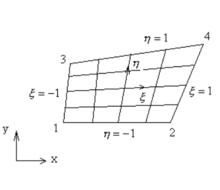
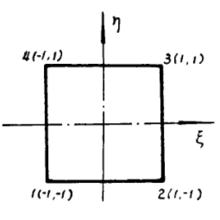
取四个角点为结点,在单元内的排序为1、2、3、4。仿照矩形单元,可定义出四个形函数:
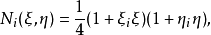 其中i=1,2,3,4。3
其中i=1,2,3,4。3
采用类似四结点矩形单元的特性分析,可以建立单元应变矩阵、应力矩阵、刚度矩阵、结点力等效的计算公式。
单元应变矩阵 其中,
其中,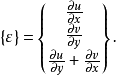
应力矩阵表达式为:[S]=[D][B].
单元刚度矩阵是一个8×8的矩阵 ,仍为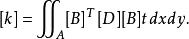 由于[B]是用局部坐标系ξ、η给出,因此
由于[B]是用局部坐标系ξ、η给出,因此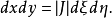 故:
故: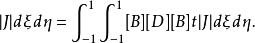
一般而言,等参单元的刚度积分很难有解析式,必须进行数值积分,普遍采用高斯数值积分法。
结点力等效将作用在单元上的外载荷同样表示为局部坐标的函数,就可以在局部坐标下完成单元的载荷移置。
体力移置的公式为:
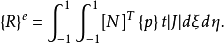
单元刚度矩阵表达式如下所示:
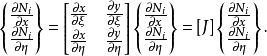 称为雅可比矩阵,由坐标变换式确定,当逆阵存在时,则形函数对x ,y 的导数可求,即应变阵可求。一般而言,等参单元的刚度积分很难有解析式,必须进行数值积分,普遍采用高斯数值积分法。2
称为雅可比矩阵,由坐标变换式确定,当逆阵存在时,则形函数对x ,y 的导数可求,即应变阵可求。一般而言,等参单元的刚度积分很难有解析式,必须进行数值积分,普遍采用高斯数值积分法。2
等参单元的几点说明:
1.等参单元为协调元,满足有限元解收敛的充要条件;
2.等参单元存在的充要条件是:∣J∣≠0;
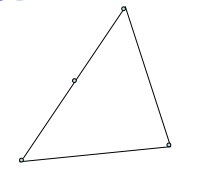
3.要求总体坐标系下的单元为凸,即不能有内角大于或等于或接近180 度情况。其中坐标系下单元为凹的多边形如图3所示,坐标系下单元为凸的多边形如图4所示:

单元特性分析与结点力计算过程与四结点等参数单元完全相同,具体公式形式也一致。区别仅在于两种单元有关矩阵的维数不同。四结点单元与八结点单元的区别如表1所示:3
表1.四结点单元与八结点单元的区别| 四结点单元 | 八结点单元 | |
| {δ} | 8×1列阵 | 16×1列阵 |
| [B] | 3×8矩阵, 4个分块 | 3×16矩阵,8个分块 |
| [k] | 8×8矩阵 | 16×16矩阵 |
| 面力 | 分到2个结点 | 分到3个结点 |




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国